Все документы,
представленные в каталоге, не являются их официальным изданием и предназначены
исключительно для ознакомительных целей. Электронные копии этих документов могут распространяться без всяких
ограничений.
Вы можете размещать информацию с этого сайта на любом другом сайте
без каких-либо ограничений.
Р 50.2.028-2003
|
РЕКОМЕНДАЦИИ ПО МЕТРОЛОГИИ |
Государственная система обеспечения единства измерений
АЛГОРИТМЫ ПОСТРОЕНИЯ ГРАДУИРОВОЧНЫХ ХАРАКТЕРИСТИК СРЕДСТВ ИЗМЕРЕНИЙ СОСТАВА ВЕЩЕСТВ И МАТЕРИАЛОВ И ОЦЕНИВАНИЕ ИХ ПОГРЕШНОСТЕЙ (НЕОПРЕДЕЛЕННОСТЕЙ)
Оценивание погрешности (неопределенности) линейных градуировочных характеристик использовании метода наименьших квадратов
ГОССТАНДАРТ РОССИИ
Москва
Предисловие
1 РАЗРАБОТАНЫ Федеральным государственным унитарным предприятием «Всероссийский научно-исследовательский институт метрологии им. Д.И. Менделеева» (ФГУП «ВНИИМ им. Д.И. Менделеева») Госстандарта России
ВНЕСЕНЫ Управлением метрологии Госстандарта России
2 ПРИНЯТЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ Постановлением Госстандарта России от 14 мая 2003 г. № 142-ст
3 ВВЕДЕНЫ ВПЕРВЫЕ
Содержание:
|
РЕКОМЕНДАЦИИ ПО МЕТРОЛОГИИ |
|
Государственная система обеспечения единства измерений АЛГОРИТМЫ ПОСТРОЕНИЯ ГРАДУИРОВОЧНЫХ ХАРАКТЕРИСТИК СРЕДСТВ ИЗМЕРЕНИЙ СОСТАВА ВЕЩЕСТВ И МАТЕРИАЛОВ И ОЦЕНИВАНИЕ ИХ ПОГРЕШНОСТЕЙ (НЕОПРЕДЕЛЕННОСТЕЙ) Оценивание погрешности (неопределенности) линейных градуировочных характеристик использовании метода наименьших квадратов |
Дата введения 2004-01-01
1 Область применения
Настоящие рекомендации распространяются на методы планирования измерительного эксперимента и оценивания характеристик погрешности (неопределенности) построения линейных градуировочных характеристик средств измерений состава веществ и материалов (ГХ СИ) методом наименьших квадратов (МНК).
2 Определения и обозначения
2.1 В настоящих рекомендациях применены следующие термины с соответствующими определениями:
градуировочная характеристика средства измерения состава веществ и материалов: Функциональная зависимость между входной (х) и выходной (y) величинами, построенная на основе значений градуировочных смесей и результатов измерений соответствующих выходных величин в N точках диапазона измерений (хi, уij), где i = 1,…, N; j = 1,…, n [1], [2];
оценка стандартной неопределенности по типу А: Оценка на основании результатов многократных измерений [1], [2];
оценка стандартной неопределенности по типу В: Оценка на основании априорной информации [1], [2].
2.2 В настоящих рекомендациях применены следующие обозначения:
S (y) - среднее квадратическое отклонение (СКО) однократного измерения выходной величины;
S (![]() ) - СКО
среднего значения выходной величины;
) - СКО
среднего значения выходной величины;
uA (![]() ) - стандартная неопределенность среднего значения выходной величины,
оцененная по типу А;
) - стандартная неопределенность среднего значения выходной величины,
оцененная по типу А;
uB (![]() ) - стандартная неопределенность среднего значения выходной величины,
оцененная по типу В;
) - стандартная неопределенность среднего значения выходной величины,
оцененная по типу В;
uB (x) - стандартная неопределенность градуировочной смеси, оцененная по типу В;
Sθ (х) - СКО неисключенной систематической погрешности градуировочных смесей;
SΣ (х) - СКО погрешности построения ГХ СИ в точке х;
uΣ (х) - суммарная стандартная неопределенность построения ГХ СИ в точке х
Up (х) - расширенная неопределенность построения ГХ СИ в точке х;
cov (xi, хj) - ковариация погрешностей i, j градуировочных смесей;
ГХ - градуировочная характеристика;
СИ - средство измерения.
3 Построение линейных градуировочных характеристик средств измерений (ГХ СИ) методом наименьших квадратов (МНК)
3.1 Исходными данными для построения ГХ СИ являются результаты измерений (хi, уij), где i = 1,…, N; j = 1,…, n.
3.2 ГХ СИ задается в виде:
![]() , (1)
, (1)
где
![]() . (2)
. (2)
3.3 Оценки параметров ГХ СИ вычисляют по формулам:
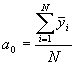 , (3)
, (3)
 , (4)
, (4)
![]() . (5)
. (5)
4 Оценивание характеристик погрешности (неопределенности) построения ГХ СИ*
4.1 Источниками погрешности (неопределенности) построения ГХ СИ являются:
- случайные погрешности измерения выходной величины уij,
- систематические погрешности градуировочных смесей хi,
4.2 Оценивание СКО (стандартной неопределенности) случайной погрешности измерения выходной величины
* В ФГУП «ВНИИМ им. Д.И. Менделеева» разработана программа обработки данных и оценивания характеристик погрешности (неопределенности) построения градуировочных характеристик средств измерений в соответствии с настоящими Рекомендациями.
4.2.1 При многократных равноточных измерениях (независимость СКО от точки диапазона) СКО (стандартную неопределенность) выходной величины у вычисляют на основании экспериментальных данных (оценивание по типу А) по формуле:
![]()
 . (6)
. (6)
4.2.2 При однократных измерениях СКО (стандартная неопределенность) выходной величины у может быть рассчитана по типу В, используя паспортные данные средства измерения о сходимости показаний, по формуле:
![]() , (7)
, (7)
где Sсход - СКО случайной погрешности средства измерения.
4.3 СКО систематической погрешности (стандартную неопределенность) градуировочных смесей обычно оценивают на основании информации о границах допустимых погрешностей градуировочных смесей (по типу В) по формулам:
![]() (8)
(8)
если нормируют абсолютные погрешности [Ө(x)] градуировочных смесей;
![]() (9)
(9)
если нормируют относительные погрешности [δ(x)] градуировочных смесей.
4.4 Оценивание корреляции между погрешностями градуировочных смесей
4.4.1 Если градуировочные смеси готовились независимо, то в большинстве случаев можно считать их погрешности независимыми, в этом случае коэффициент корреляции равен нулю и ковариацию оценивают по формуле:
![]() .
.
4.4.2 Если градуировочные смеси готовились разбавлением основной смеси или с использованием одних и тех же стандартных образцов, то корреляция между погрешностями их приготовления может достичь 1, что соответствует присутствию постоянной систематической погрешности градуировочных смесей, в этом случае ковариацию оценивают по формуле:
![]() .
.
4.5 Оценивание СКО погрешности (суммарной стандартной неопределенности) построения ГХ СИ
4.5.1 Если корреляция погрешностей градуировочных смесей отсутствует и характеристики абсолютных погрешностей градуировочных смесей остаются постоянными на всем диапазоне изменения входной величины, то СКО погрешности (суммарную стандартную неопределенность) построения ГХ СИ вычисляют по формуле:
 , (10)
, (10)
где θ - границы абсолютных погрешностей градуировочных смесей.
Если корреляция погрешностей градуировочных смесей отсутствует, а характеристики погрешности градуировочных смесей зависят от точки диапазона, то СКО погрешности (суммарную стандартную неопределенность) построения ГХ СИ вычисляют по формуле:
 , (11)
, (11)
где θ (х) - границы абсолютных погрешностей градуировочных смесей в точке х.
4.5.2 Если корреляция погрешностей градуировочных смесей присутствует и характеристики абсолютных погрешностей градуировочных смесей остаются постоянными на всем диапазоне изменения входной величины, то СКО погрешности (суммарную стандартную неопределенность) построения ГХ СИ вычисляют по формуле:
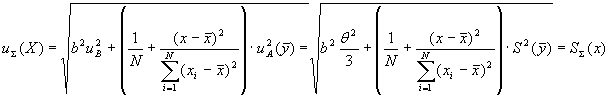 (12)
(12)
Если присутствует корреляция погрешностей градуировочных смесей, а характеристики погрешностей градуировочных смесей зависят от точки диапазона, то СКО погрешности (суммарную стандартную неопределенность) построения ГХ СИ вычисляют по формуле:
 , (13)
, (13)
4.6 При вычислении доверительных границ погрешности (расширенной неопределенности) построения ГХ СИ рекомендуется использовать следующие коэффициенты охвата k:
k = 2 - при доверительной вероятности Р = 0,95;
k = 3 - при доверительной вероятности Р = 0,99.
Доверительные границы (расширенную неопределенность) вычисляют по формуле:
![]() .
(14)
.
(14)
5 Планирование измерений при построении линейных ГХ СИ
5.1 Планирование измерений направлено на оптимизацию затрат при проведении измерений для достижения требуемой точности построения ГХ СИ и проводится на этапе разработки методик выполнения измерений. Планирование измерений заключается в выборе числа параллельных измерений в точке n, числа градуировочных точек N, а также установлении требований к точности градуировочных смесей, исходя из требуемой точности построения градуировочной характеристики. Ниже приводится одно из возможных простых решений задачи планирования измерений. После выбора числа параллельных измерений в точке n, числа градуировочных точек (N), а также точности градуировочных смесей оценивание характеристик погрешности (неопределенности) ГХ СИ следует проводить в соответствии с разделом 4.
5.2 Число измерений n в точке рационально выбирать из условия незначительного (не более 20 %) роста суммарной погрешности по сравнению с систематической составляющей по формуле:
![]() . (15)
. (15)
5.3 Если погрешности градуировочных смесей не коррелированы, то требуемая точность построения ГХ СИ может быть достигнута за счет увеличения числа градуировочных смесей и уменьшения их погрешностей в соответствии с формулой:
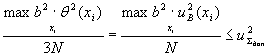 , (16)
, (16)
где uΣдоп - допустимая суммарная стандартная неопределенность построения ГХ СИ (СКО допустимой погрешности).
5.4 Если погрешности градуировочных смесей коррелированы, то при построении линейных ГХ СИ рекомендуется использовать две градуировочные смеси. При этом должны быть обеспечены следующие погрешности градуировочных смесей, исходя из требований к точности построения ГХ СИ:
 (17)
(17)
6 Контроль стабильности ГХ СИ
6.1 Обычно процедура контроля стабильности ГХ СИ состоит в сравнении измеренного значения выходного сигнала в градуировочных точках с его оценкой по ГХ СИ (данный результат измерения не используется при построении ГХ СИ). Для линейной ГХ СИ число точек контроля должно быть не менее двух.
6.2 Если погрешности градуировочных смесей не коррелированы, то проверяют следующие условия в соответствии с формулами:
![]() при N ≥
5; (18)
при N ≥
5; (18)
![]() при N ≤
4, (19)
при N ≤
4, (19)
где yi - измеренное значение выходного сигнала в точке хi,
![]() - оценка выходного сигнала по
ГХ СИ в точке хi.
- оценка выходного сигнала по
ГХ СИ в точке хi.
6.3 Если погрешности градуировочных смесей коррелированы, то проверяют следующие условия в соответствии с формулами:
![]() при N ≥
5; (20)
при N ≥
5; (20)
![]() при N ≤
4, (21)
при N ≤
4, (21)
ПРИЛОЖЕНИЕ А
(рекомендуемое)
Пример построения градуировочной характеристики
А. 1 Исходные данные
Градуировочная характеристика хроматографа строится по стандартным образцам водных растворов этанола массовой концентрации хi (N = 7). Границы относительной погрешности массовой концентрации этанола не превышают 0,5 %. Выполняют по 5 параллельных измерений в каждой точке (n = 5). Данные для построения градуировочной характеристики приведены в таблице А.1.
Таблица А.1
|
Обозначение параметра |
Значения массовой концентрации (входная величина) |
||||||
|
xi, мг/мл |
0,49 |
0,97 |
2,00 |
2,96 |
4,05 |
5,07 |
6,05 |
|
Результаты измерения |
|||||||
|
yij |
227451 |
439935 |
942200 |
1404433 |
1821194 |
2277460 |
2824679 |
|
221585 |
454170 |
935664 |
1391932 |
1825116 |
2240900 |
2825947 |
|
|
232387 |
444558 |
929875 |
1409124 |
1874371 |
2275484 |
2834183 |
|
|
223216 |
453812 |
933705 |
1385680 |
1834334 |
2319111 |
2816202 |
|
|
233628 |
457800 |
937104 |
1375168 |
1802673 |
2180685 |
2853467 |
|
|
Средние значения выходного сигнала в i-й точке |
|||||||
|
|
227653 |
450055 |
935710 |
1393267 |
1831538 |
2258728 |
2830896 |
|
СКО единичного измерения выходного сигнала в i-й точке |
|||||||
|
Si |
5353,965 |
7477,712 |
4531,355 |
13811,61 |
26208,11 |
51687,29 |
14136,05 |
А.2 Вычисление коэффициентов градуировочной характеристики
Градуировочная характеристика представлена в виде:
![]() ; (А.1)
; (А.1)
![]() . (А.2)
. (А.2)
Оценки градуировочных коэффициентов вычисляют по формулам:
 , (А.3)
, (А.3)
 , (А.4)
, (А.4)
![]() . (А.5)
. (А.5)
А.3 Оценивание погрешности (неопределенности) построения градуировочной зависимости
Оценку СКО (стандартную неопределенность по типу А) выходного сигнала в предположении равноточности измерений получают по формуле:
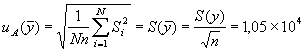 , (А.6)
, (А.6)
где ![]()
Оценку СКО систематической погрешности (стандартной неопределенности по типу В) градуировочной смеси, которое в данном случае зависит от значения градуировочной смеси, вычисляют по формуле:
![]() , (А.7)
, (А.7)
где δ(х) = 0,5 % - границы относительной погрешности массовой концентрации этанола. Оценку СКО суммарной погрешности (суммарной стандартной неопределенности) построения градуировочной характеристики вычисляют по формуле:
 , (А.8)
, (А.8)
где ![]() ;
;
![]()
![]()
Доверительные границы погрешности (расширенную неопределенность) построении градуировочной характеристики вычисляют по формуле:
![]() . (А.9)
. (А.9)
ПРИЛОЖЕНИЕ Б
(справочное)
Библиография
[1] МИ 2175-91 Государственная система обеспечения единства измерений. Градуировочные характеристики средств измерений. Методы построения, оценивание погрешностей
[2] РМГ 43-2001 Государственная система обеспечения единства измерений. Применение «Руководства по выражению неопределенности измерений»
|
Ключевые слова: средство измерений состава веществ, линейная градуировочная характеристика, построение градуировочной характеристики, метод наименьших квадратов, погрешность, неопределенность, оценивание погрешности (неопределенности), среднее квадратическое отклонение. |
|
|||||||||||||||||||||