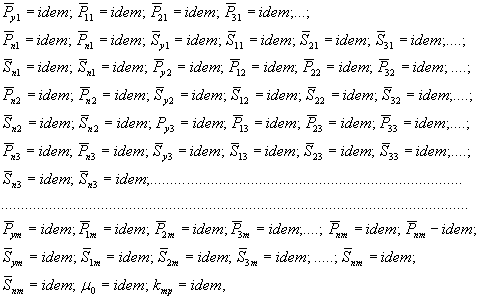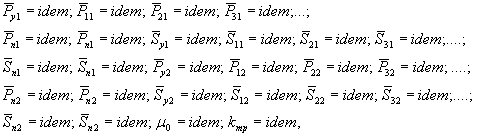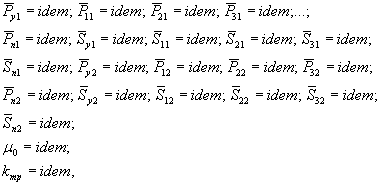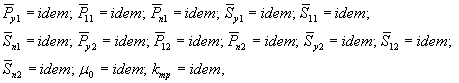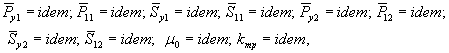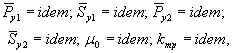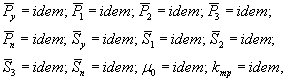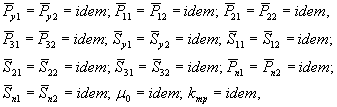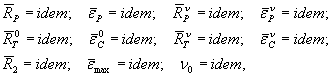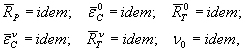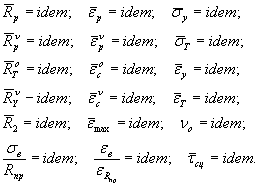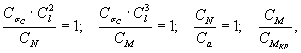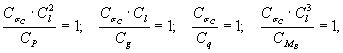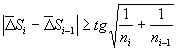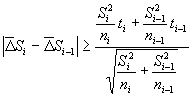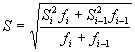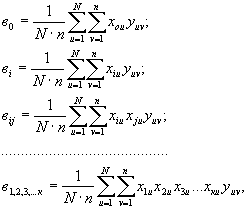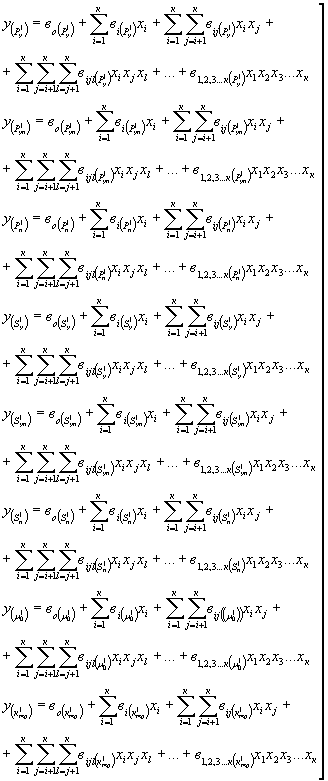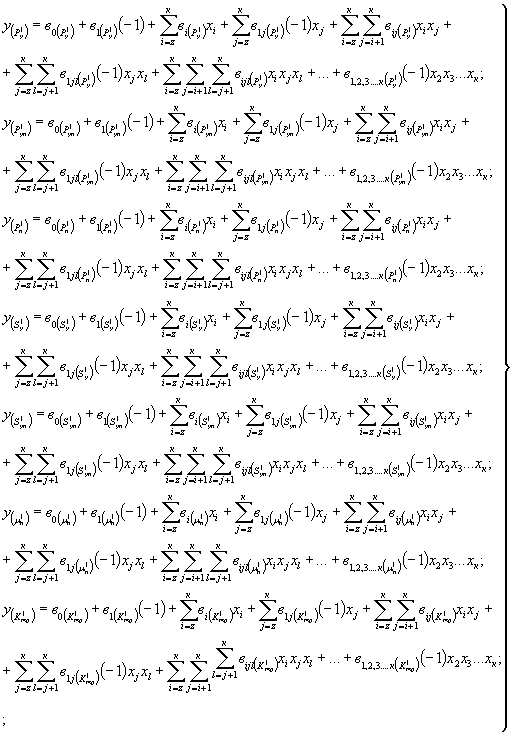Все документы,
представленные в каталоге, не являются их официальным изданием и предназначены
исключительно для ознакомительных целей. Электронные копии этих документов могут распространяться без всяких
ограничений.
Вы можете размещать информацию с этого сайта на любом другом сайте
без каких-либо ограничений.
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ ГОССТРОЯ СССР
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО МОДЕЛИРОВАНИЮ ГРУНТОВОГО ОСНОВАНИЯ ПРИ ИССЛЕДОВАНИИ
НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ СООРУЖЕНИЯ
Одобрены секцией № 1 Научно-технического совета НИИСКГосстроя СССР
Протокол № 12 от 29 октября 1980 г.
НИИСК, КИЕВ 1981
СОДЕРЖАНИЕ
Изложены рекомендации по моделированию напряженно-деформированного состояния сооружения на грунтовом оснований. Приведены критерии подобия грунтового основания и системы "сооружение-основание", условия моделирования, методы определения параметрических точек на графике "осадка-давление", методика получения материала грунтового основания модели с заданными свойствами. Даны примеры моделирования.
Предназначены для научных работников строительного профиля.
Рекомендации разработаны инж. В.Г. Тарасюком и канд. техн наук Г.В. Шараповым (НИИСК Госстроя СССР).
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Метод моделирования является эффективным средством исследования пространственных систем, проведение расчета которых с учетом всех их особенностей (сложные граничные условия, совместная работа с основанием и т.д.) во многих случаях встречает серьезные затруднения. Метод моделирования позволяет провести качественное и количественное исследование напряженно-деформированного состояния конструкций, оценить достоверность методов их расчета, распространить результаты единичных опытов на рассматриваемый класс систем.
1.2. Настоящие рекомендации относятся к моделированию напряженно-деформированного состояния сооружения на грунтовом оснований с учетом стадий работы материалов, из которых состоит система "сооружение-основание". Сооружения из грунта не рассматриваются.
1.3. Приведенные ниже положения распространяются на сооружения с фундаментами под отдельно стоящие колонны, ленточными фундаментами, фундаментами значительных размеров, а также их различными сочетаниями при статическом действии нагрузки.
1.4. При установлении подобия процессов, происходящих в оригинале и модели, использована теория расширенного подобия [l]. Критерии подобия напряженно-деформированного состояния сооружения на грунтовом основании получены для системы "сооружение-основание" как составного тела. Подобие материалов сооружения рассматривается исходя из подобия индикаторных диаграмм σ - ε. Критерии подобия грунтового основания при исследовании напряженно-деформированного состояния сооружения получены на основании графиков F - S штамповых испытаний.
1.5. В стадии разрушения доверительные интервалы осадки в зависимости от давления значительно больше, чем в упругой стадии работы основания. Поэтому предлагаемый метод в стадии разрушения грунтового основания менее точен, чем в упругой.
1.6. В отличие от положений, изложенных в [1], гомогенность диаграмм рассматривается не на всем участке, а в параметрических и дополнительных точках.
1.7. В соответствии с положениями о подобия составных тел [1-2] при моделировании напряженно-деформированного состояния сооружения на грунтовом основании необходимо выполнять следующие условия подобия:
геометрические;
для материалов сооружения и основания;
статические;
по контактной поверхности сооружения и основания.
Невыполнение хотя бы одного из этих условий может привести к существенным погрешностям в оценке действительного напряженно-деформированного состояния сооружения, полученного на основании испытаний на моделях,
1.8. Под геометрическими условиями подобия следует понимать полное геометрическое подобие сооружения и основания.
2. КРИТЕРИИ ПОДОБИЯ МАТЕРИАЛОВ СИСТЕМЫ ''СООРУЖЕНИЕ-ОСНОВАНИЕ"
2.1. Критерии подобия грунтового основания
2.1.1. Согласно положениям СНиП II-15-74 расчет основания производится по несущей способности и по предельным деформациям. Как правило, определяющим является расчет по предельным деформациям, в значительной степени определяющий напряженно-деформированное состояние сооружения. Поэтому рассматривается не полное подобие напряженно-деформированного состояния основания, а моделируются его осадки.
2.1.2. Основание сооружения является составной частью системы "сооружение-основание". Поэтому правильное определение критериев подобия основания и их выполнение в значительной степени влияют на конечный результат исследований системы в целом. Согласно [3] при определении механических характеристик грунта необходимо выполнить следующие требования:
свойства образцов должны соответствовать состоянию грунта в естественном залегании;
граничные и временные условия загружения и деформирования грунта при его работе в сооружении должны моделироваться при испытаниях.
2.1.3. Рассматривая работу грунта под фундаментами зданий и сооружений, следует отметить, что наиболее полно выполняются вышеназванные требования при штамповых испытаниях грунта пробными нагрузками. Поэтому в основу определения деформированных характеристик грунта при изучении на моделях напряженно-деформированного состояния сооружения на грунтовом основании были положены штамповые испытания.
2.1.4. В соответствии с п. 1.4, чтобы получить материал основания, подобный оригиналу, необходимо иметь закон взаимосвязи напряжений и деформаций для оригинала, полученный при испытании образцов из материала оригинала при заданном законе загружения. Это свидетельствует о том, что для получения критериев механического подобия оснований большое значение имеют анализ и выяснение физической сущности связи напряжений и деформаций в грунтовых основаниях.
2.1.5. Учитывая класс рассматриваемых задач, в качестве исходной информации для установления подобия грунтового основания принимаем зависимость осадки от давления, получаемую в результате штамповых испытаний. При этом исходим из следующих соображений:
график Р - S структурно подобен диаграмме σ - ε;
удельное давление Р интегрально характеризует нормальное контактное напряжение под штампом и является осредненной величиной значений нормальных контактных напряжений;
осадка штампа S и величина Δl - εl сходственны между собой.
В соответствии с этим подобие материалов грунтовых оснований следует трактовать как подобие их графиков штамповых испытаний.
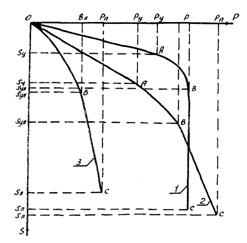
Рис. 1. Параметрические точки и их координаты на графиках штамповых испытаний
1, 2, 3 - основные типы зависимостей осадки от давления
2.1.6. Возможные графики штамповых испытаний, приведенные на основе данных работы [5], показаны на рис. 1. Кривая 1 характерна для фундаментов мелкого заложения на плотных грунтах. Зависимость 2 характерна для глинистых грунтов и песков средней плотности, а также для плотных грунтов при фундаментах глубокого заложения. График В характерен для слабых грунтов. Анализируя графики Р - S, приведенные на рис. 1, можем отметить, что для кривых 1 и 2 характерно наличие линейного участка ОА. Линейную зависимость Р - S характеризует некоторое уплотнение грунта, медленное развитие зон сдвигов. Эту фазу работы основания с достаточной степенью точности можно принять линейной. Следовательно, точка А с координатами РY и SY, являющаяся границей линейной работы основания, может быть принята в качестве параметрической. Участок АВ (ОВ для кривой 3) характеризуется более интенсивным развитием зон сдвигов. Перемещение основания носит значительный характер. В конце участка завершается процесс формирования упругого ядра. Эта фаза работы основания принята нелинейной. Точна В с координатами РУП и SУП является второй параметрической точкой. Участок ВС характеризует разрушение основания. Штамп вместе с упругим ядром раздвигает грунт и резко перемещается вниз, получая значительную, но конечную осадку. Точка С с координатами РП и SП определяет окончательное перемещение штампа и является третьей параметрической точкой графика Р - S.
Следовательно, в общем случае для графика штамповых испытаний характерно наличие трех фаз работы, а именно: линейной, нелинейной и стадии разрушения. Причем графику Р - S характерно наличие параметрических точек, определяющих фазы работы основания. Координаты этих точек определяют деформативные и прочностные свойства основания под штампом.
2.1.7. На основе теории расширенного подобия [1] для моделирования работы грунтовых оснований при исследовании напряженно-деформированного состояния сооружения на моделях необходимо выполнение условий:
|
|
где ![]() - масштабный
множитель нормальных контактных напряжений; СS - масштабный множитель осадок.
- масштабный
множитель нормальных контактных напряжений; СS - масштабный множитель осадок.
Штрихованная система относится к материалу модели, а нештрихованная - к материалу оригинала.
2.1.8. Для успешного проведения работ по моделированию работы сооружений на грунтовом основании большое значение имеет установление практических критериев подобия материала основания в зависимости от цели исследований. В этом случае условия системы (1) обеспечат полное подобие материала основания только в определенных зонах графика Р - S и неполное - в остальных.
2.1.9. Для получения работы здания или сооружения при упругой стадии работы материалов основания из: условий (1) достаточно удовлетворить:
|
|
(2) |
2.1.10. При изучении работы сооружения на грунтовом основании, которое находится в стадии разрушения, из условий подобия грунтовых оснований модели и оригинала (1) необходимо удовлетворить условия:
|
|
(3) |
Если же график Р - S описывается кривой 1 (см. рис. 1), то условия подобия имеют вид:
|
|
(4) |
2.1.11. Для моделирования работы основания в упругопластической стадии при условии адекватности графиков штамповых испытаний модели и оригинала в данной области работы грунтового основания требуется выполнение условий:
|
|
(5) |
2.1.12. При исследовании напряженно-деформированного состояния сооружения, когда основание находится в нелинейной стадии своей работы, подобие графиков Р' - S' и Р - S в точках А и В, характеризующих границы нелинейной стадии работы основания, может оказаться недостаточным (рис. 2,а). В этом случае для повышения достоверности результатов исследования на моделях необходимо на участке АВ графиков P' - S' и P - S ввести дополнительные точки (см. рис. 2,б - 2,г). В идеале, увеличивая количество точек до бесконечности, можем добиться полного совпадения участка графиков штамповых испытаний материала основания модели и оригинала. Следовательно, для достижения подобия материалов грунтового основания необходимо выполнение условий:
 ;
;
(6)
![]()
![]() ;
;
где индексами от 1 до п обозначены координаты дополнительных точек на графиках штамповых испытаний в нелинейной стадии работы материалов грунтовых оснований.
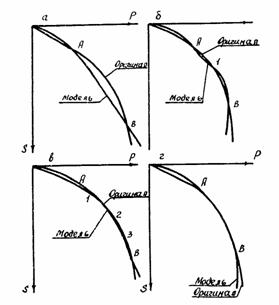
Рис. 2. Дополнительные точки в нелинейной стадии работы материалов
а - при наличии точек А и В; б - при наличии одной дополнительной точки; в - при наличии нескольких дополнительных точек; г - при количестве дополнительных точек, равном бесконечности
2.1.13. В общем случае, если исследователя интересует работа основания на всем диапазоне загружения, необходимо выполнение условий:
![]() ;
;
(7)
![]() ,
,
2.1.14. При подборе
материалов, моделирующих грунтовое основание, масштабные множители ![]() и CS
заранее неизвестны. Поэтому условием (7) пользоваться непосредственно не всегда
удобно. Для получения критериев подобия материалов оснований сооружений в
форме, удобной для подбора модельных материалов, гомогенные графики P - S и P' – S' представим в относительной
системе координат:
и CS
заранее неизвестны. Поэтому условием (7) пользоваться непосредственно не всегда
удобно. Для получения критериев подобия материалов оснований сооружений в
форме, удобной для подбора модельных материалов, гомогенные графики P - S и P' – S' представим в относительной
системе координат:
![]() .
.
и
![]() .
.
Тогда условие
гомогенности функций S = f(P) и S' = f'(P') превращается в равенство ![]() , которое выполняется при равенстве относительных координат
соответствующих параметрических или параметрических и дополнительных точек,
, которое выполняется при равенстве относительных координат
соответствующих параметрических или параметрических и дополнительных точек,
2.1.15. Для графика типа 1 (см. рис. 1) условие подобия примет вид:
![]()
|
|
(8) |
![]() .
.
Для графика типа 2 (см. рис. 1) условие подобия оснований примет вид
![]()
|
|
(9) |
![]() .
.
Для графика типа 3 (см. рис. 1) имеем:
![]()
|
|
(10) |
![]() .
.
Сравнивая вышеприведенные системы критериев подобия, приходим к заключению, что система (9) носит общий характер для всех трех случаев.
2.1.16. Система критериев подобия (9) является неполной. Расширенное подобие, как и простое, предусматривает равенство коэффициентов поперечной деформации (коэффициентов Пуассона) для материалов модели и оригинала и, в соответствии с условиями подобия составных систем, одинаковость сопряжения элементов системы. В качестве интегральной характеристики, обеспечивающей одинаковость условий сопряжения сооружения и основания, принят коэффициент трения подошвы фундамента (штампа) по поверхности основания.
2.1.17. С учетом п. 2.1.17 система критериев подобия (9)примет вид:
![]()
|
|
(11) |
![]()
![]() ,
,
где μ0 - коэффициент Пуассона; kтр - коэффициент трения по контактной поверхности фундамента и основания.
Приведенные критерии подобия грунтового основания при моделировании напряженно-деформированного состояния сооружения на грунтовой основании являются необходимыми и достаточными при условии, что размер штампа соответствует размеру фундамента.
2.1.18. В соответствии с положениями теории упругости между осадкой штампа и его размером должна существовать линейная зависимость. Однако, согласно экспериментальным данным [6] зависимость между осадкой и размером фундамента описывается более сложной кривой (рис. 3). На участке ab с увеличением размера штампа осадка уменьшается, что объясняется преобладающей ролью деформаций сдвига над деформациями уплотнения. На участке сd увеличением размера штампа осадки нарастают за счет того, что грунт находится, в основном, в фазе уплотнения. При дальнейшем увеличении размера штампа осадка нелинейно возрастает, а начиная с определенного размера (участок ef), осадка не зависит от размера штампа. Поэтому для получения не только необходимых, но и достаточных критериев подобия основания нужно учитывать влияние размера фундамента на осадку.

Рис. 3. Зависимость осадки штампа от его линейных размеров при постоянном давлении
2.1.19. Для учета в процессе исследования на моделях влияния размера фундамента на осадку необходимо иметь график штамповых испытаний Р - S материала основания оригинала не для одного какого-либо размера штампа, а для целого ряда. Этот ряд должен подбираться из условия, чтобы графики Р - S были получены для штампов, где осадка состоит, в основном, из деформаций сдвига, уплотнения и случая, когда осадка не зависит от размера фундамента. Таким образом, исходной информацией для установления подобия материалов основания оригинала и модели будет целый ряд графиков Р - S штамповых испытаний, захватывающих области аb (см. рис. 3), bc, de и некоторую часть области ef.
2.1.20. Выделив на каждом
из полученных графиков штамповых испытаний Р
- S параметрические и дополнительные в нелинейных фазах точки,
представим их в безразмерных координатах ![]() -
- ![]() . Тогда координаты параметрических и дополнительных точек
графиков штамповых испытаний
. Тогда координаты параметрических и дополнительных точек
графиков штамповых испытаний ![]() -
- ![]() , дополненные значениями μ0
= idem и kтр = idem, будут представлять собой
необходимые и достаточные критерии подобия грунтового основания при
моделировании работы сооружения на грунтовом основании. Критерии подобия
однорядного грунтового основания в общем случае при моделировании
напряженно-деформированного состояния сооружения на грунтовом основании имеют
вид:
, дополненные значениями μ0
= idem и kтр = idem, будут представлять собой
необходимые и достаточные критерии подобия грунтового основания при
моделировании работы сооружения на грунтовом основании. Критерии подобия
однорядного грунтового основания в общем случае при моделировании
напряженно-деформированного состояния сооружения на грунтовом основании имеют
вид:
|
|
(12) |
где второй цифрой oт до m при индексе обозначается номер штампа, определяемый его размером. Наименьшему штампу присвоен первый номер, наибольшему - m.
2.1.21. Как и в случае единичных штамповых испытаний [7], в рассматриваемом наиболее общем случае решающее значение имеют практические критерии подобия материалов оснований в зависимости от целей исследований и размеров фундамента,
2.1.22. Участок cd (см. рис. 3) характеризуется линейной зависимостью между осадкой и размером фундамента при постоянном давлении. Размер стороны фундамента в этом случае колеблется в пределах 0,5 - 7,0 м [8]. В результате [9 - 14] можно заключить, что для моделирования работы основания под квадратным, круглым, прямоугольным и ленточным фундаментами шириной до 7,0 м в качестве исходной информации необходимо иметь два графика Р - S. соответствующие работе основания под штампами, находящимися в зоне линейной зависимости осадки от размера штампа.
Следовательно, для установления подобия на всем диапазоне работы основания при фундаментах шириной до 7 м необходимо выполнение критериев:
|
2.1.23. При проведении исследований на моделях сооружений с фундаментами шириной до 7 м с использованием материала основания на всем диапазоне загружения (линейная и нелинейная стадии, и стадия разрушения) и при наличии трех дополнительных точек в нелинейной стадий работы основания на графиках Р - S в линейной области зависимости осадка от размера фундамента необходимо выполнение следующих критериев подобия:
|
|
(14) |
2.1.24. При необходимости одной дополнительной точки в нелинейной стадии работы основания в линейной области зависимости осадки от размера фундамента критерии подобия примут следующий вид:
|
|
(15) |
2.1.25. При проведении исследований в линейной и нелинейной стадиях работы основания с одной дополнительной точкой в нелинейной фазе в линейной области зависимости осадки от размера фундамента необходимо выполнение критериев:
|
|
(16) |
2.1.26. Для исследования работы сооружения с учетом только линейной стадии работы основания в линейной области зависимости осадки от размера фундамента критерии подобия примут вид:
|
|
(17) |
2.1.27. При исследовании на моделях напряженно-деформированного состояния сооружения с фундаментами под отдельно стоящие колонны или ленточными фундаментами на грунтовом основании возможно использование в качестве исходной информации графика Р - S для штампа размером, равным ширине фундамента. В этом случае критериями подобия грунтового основания являются координаты параметрических и дополнительных точек одного графика Р - S и равенство в модели и оригинале коэффициента Пуассона и коэффициента трения по контактной поверхности фундамента и основания (см. систему (11).
2.1.28. Рассматривая ту же задачу, что и в п. 2.1.27, но с использованием трех дополнительных точек в нелинейной стадии, критерии подобия грунтового основа - можем представить следующим образом:
|
|
(18) |
2.1.29. При проведении исследований в линейной зоне работы основания критерии подобия (18) примут следующий вид:
|
|
(19) |
2.1.30. Для получения условий подобия однородного грунтового основания при моделировании напряженно-деформированного состояния здания или сооружения с фундаментом значительных размеров следует в качестве исходной информации использовать графики Р - S двух штампов. Причем штампы должны быть таких размеров, чтобы при их помощи можно было зафиксировать зону, где осадка не зависит от размеров фундамента, то есть на участке ef (см. рис.3).
Тогда критерии подобия однородного грунтового основания при трех дополнительных точках в нелинейной зоне работы основания будут иметь вид:
|
2.1.31. Рассматривая ту же задачу, что и в п.2.1.30, но в линейной стадии работы основания, систему (20) сводим к виду:
|
2.1.32. Основание сооружения в природе очень часто встречается в виде неоднородной грунтовой толщи, то есть грунты залегают слоями, часто сильно отличающимися друг от друга по своим физико-механическим характеристикам. Поэтому при моделировании напряженно-деформированного состояния сооружения на неоднородном грунтовом основании необходимо учитывать особенности отдельных слоев грунта, их мощность и взаимное расположение.
2.1.33. Рассматривая неоднородное грунтовое основание с горизонтальным или близким к горизонтальному расположением слоев грунта как составное тело, получим, что для подобия неоднородных оснований модели и оригинала необходимо выполнение условий:
геометрического подобия каждого из слоев;
критериев подобия вида (12) для каждого из слоев;
критериев подобия, обеспечивающих совместность работы слоев основания, которые имеют вид:
|
|
(22) |
k12 = idem; k23 = idem;….; kn-1n = idem,
где σоп - контактное напряжение под штампом слоя п;
Son - осадка штампа слоя п;
Kn-1n - коэффициент трения по поверхности соприкасания двух слоев грунта.
2,1.34. В случае, если мощности слоев грунта, составляющие неоднородное основание, незначительны и получить полную зависимость между осадкой и размером штампа (см. рис. 3) не представляется возможным, необходимо учитывать, что размеры фундаментов, с которыми можно проводить исследования, на моделях, также ограничены.
2.2. Критерии подобий материалов сооружения
2.2.1. На основе теории
расширенного подобия [1]
в работе [4]
получены критерии подобия бетона в механическом
смысле. В соответствии с [4] необходимым и достаточным условием подобия
материалов типа бетон в момент времени t является гомогенность
трех диаграмм: индикаторной σ - ε, состояния (изменение скорости
прохождения ультразвука) и изменения коэффициента поперечной деформации. В
системе относительных координат ![]() ,
, ![]() полная система
критериев подобия бетонов в механическом смысле, найденная из условия
гомогенности трех диаграмм, имеет вид:
полная система
критериев подобия бетонов в механическом смысле, найденная из условия
гомогенности трех диаграмм, имеет вид:
|
|
(23) |
где ![]() и
и ![]() - относительные
координаты, соответствующие границе упругой работы бетона при растяжении;
- относительные
координаты, соответствующие границе упругой работы бетона при растяжении;
![]() и
и ![]() - относительные
координаты, соответствующие пределу прочности бетона при растяжении:
- относительные
координаты, соответствующие пределу прочности бетона при растяжении:
![]() и
и ![]() - относительные
координаты, соответствующие уровню микротрещинообразования в бетоне;
- относительные
координаты, соответствующие уровню микротрещинообразования в бетоне;
![]() и
и ![]() - относительные
координаты, соответствующие уровню макротрещинообразования в бетоне;
- относительные
координаты, соответствующие уровню макротрещинообразования в бетоне;
![]() и
и ![]() - относительные координаты,
соответствующие границе ниспадающей ветви диаграмм бетона;
- относительные координаты,
соответствующие границе ниспадающей ветви диаграмм бетона;
ν0 - коэффициент поперечной деформации бетона.
2.2.2. В. зависимости от конкретных задач в работе [4] установлены практические системы критериев подобия. Наиболее распространенной задачей механического моделирования является исследование прочности, жесткости и трещиностойкости железобетонных конструкций. Система критериев подобия бетона в этом случае будет иметь вид:
|
|
(23) |
2.2.3. Железобетон представляет собой составное тело. Поэтому при получении условий подобия для него не достаточно подобие только бетона, необходимо соблюдать условие подобия и для арматуры.
2.2.4, Критерии подобия арматуры устанавливаются также на основании расширенного подобия. Как видно из рис. 4, диаграммы σ - ε растяжения образцов арматурных сталей различны.
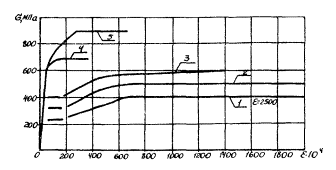
Рис. 4. Диаграммы растяжения некоторых видов арматурных сталей
1 - стержневая горячекатаная гладкая арматура класса A-I; 2 - стержневая горячекатаная арматура периодического профиля класса А-II; 3 - стержневая горячекатаная арматура периодического профиля класса А-III; 4 - обыкновенная арматурная проволока класса B-I; 5 - стержневая горячекатаная арматура периодического профиля класса А-IV
Так, для "мягких" сталей характерно наличие ярко выраженной площадки текучести. У "твердых" арматурных сталей площадка текучести практически отсутствует. В то же время независимо от класса арматурной стали в соответствии с [15] на любой индикаторной диаграмме можно выделить три параметрические точки. Такими точками являются:
условный предел упругости σν;
предел текучести (физический или условный) σт;
временное сопротивление σв.
Условный предел упругости σν и временное сопротивление σв определены однозначно для всех классов арматурных, сталей. Физический предел текучести арматурных сталей может быть найден по правилам определения условного предела текучести. При таком подходе параметрические точки, как для "твердых", так и для "мягких" арматурных сталей, могут быть определены однозначно. Принятая предпосылка дает возможность перейти от многообразия индикаторных диаграмм арматурных сталей к единой, условной, которая приведена на рис. 5.
2.2.5. Для обобщенной условной диаграммы растяжения арматурных сталей (см. рис. 5) характерно наличие трех параметрических точек:
точка А с координатами σу, εy, определяющая границу упругой работы арматурных сталей;
точка В с координатами σT, εT, определяющая границу упруго-пластической стадии работы арматурных сталей;
точка С с координатами σв, εв, определяющая момент разрушения арматурных сталей.
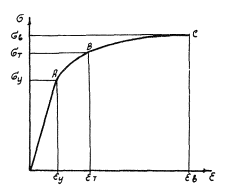
Рис. 5. Обобщенная условная диаграмма растяжения арматурных сталей
2.2.6. Параметры σν, σT. σв являются обобщенными и определяют прочностные свойства арматурных сталей, от них зависит закономерность деформирования и прочности арматурных сталей при кратковременном и длительном нагружении. Определяющие параметры находятся экспериментально путем испытания образцов арматурных сталей на одноосное растяжение.
2,2.7. Необходимым и достаточным условием подобия материалов модели и оригинала арматуры будет гомогенность диаграмм σ - ε в параметрических точках:
|
|
(25) |
2.2.8. При подборе
материалов, моделирующих работу арматуры оригинала, множители подобия ![]() и
и ![]() заранее неизвестны.
Поэтому условием (25) нельзя пользоваться непосредственно. Для вывода критериев
подобия арматуры в механической смысле в форме, удобной для подбора
моделирующих материалов, представим гомогенные диаграммы σ - ε и σ' - ε' в относительной системе координат:
заранее неизвестны.
Поэтому условием (25) нельзя пользоваться непосредственно. Для вывода критериев
подобия арматуры в механической смысле в форме, удобной для подбора
моделирующих материалов, представим гомогенные диаграммы σ - ε и σ' - ε' в относительной системе координат:
![]() и
и ![]() ,
,
Тогда условие
гомогенности функций ![]() и
и ![]() превратится в условие
равенства функций
превратится в условие
равенства функций ![]() . Это условие выполняется при равенстве относительных
координат соответствующих параметрических точек:
. Это условие выполняется при равенстве относительных
координат соответствующих параметрических точек:
|
|
(26) |
Условие (26) является системой критериев подобия арматурных сталей.
2.2.9. При исследованиях на моделях работы железобетона недостаточно выполнение критериев подобия для бетона (23) и арматурных сталей (26), так как они не учитывают совместность работы арматуры и бетона в железобетонных конструкциях. Для составного тела, которым является железобетон, необходимо, чтобы масштабные множители были одинаковыми, Данное условие выполняется при помощи критериев:
|
|
(27) |
где Rпр и ![]() - координаты на
диаграмме σ - ε, соответствующие пределу
прочности бетона при сжатии.
- координаты на
диаграмме σ - ε, соответствующие пределу
прочности бетона при сжатии.
2.2.10. Фактором, обеспечивающим совместную работу арматуры и бетона, является наличие сцепления между ними. Поэтому имеющиеся критерии подобия следует дополнить критерием, учитывающим фактор сцепления арматуры с бетоном:
|
|
(28) |
2.2.11. При исследованиях на моделях работы строительных конструкций из железобетона необходимо выполнение следующих критериев подобия:
|
|
(29) |
2.2.12. В зависимости от задач исследований количество критериев подобия для железобетона может быть уменьшено. Так, при исследовании на моделях прочности, деформативности и трещиностойкости железобетонных конструкций достаточно удовлетворение критериев:
|
|
(30) |
2.2.13. При определении границ упругой работы железобетонной конструкции материал модели должен удовлетворять критериям подобия:
|
|
(31) |
2.2.14. Для повышения точности исследований в неупругой зоне работы материалов следует вводить дополнительные точки на диаграммах σ - ε аналогично тому, как это было сделано при получении условий подобия для грунтовых оснований.
2.2.15. Критерии подобия для арматурных, сталей (26) можно использовать при исследовании на моделях работы строительных конструкций из металла, дополнив их критерием:
|
ν = idem, |
(32) |
где ν - коэффициент Пуассона металла.
3. МОДЕЛИРОВАНИЕ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ СООРУЖЕНИЯ НА ГРУНТОВОМ ОСНОВАНИИ
3.1. Условия моделирования
3.1.1. Имея критерии подобия для составляющих элементов системы "сооружение-основание" и, исходя из теории расширенного подобия составных тел [1], критерии подобия напряженно-деформированного состояния сооружения на грунтовом основании [16] имеют следующий вид:
|
|
(33) |
где σc - напряжение в сооружении; σ0 - нормальное контактное напряжение в основании; εс - деформации в сооружении; l - линейный размер; S - осадка сооружения; μc - коэффициент Пуассона материала сооружения; μ0 - коэффициент Пуассона основания; kтр - коэффициент трения по контактной поверхности сооружения и основания.
3.1.2. Условие моделирования какого-либо процесса представляет собой набор соотношений между масштабными множителями величин, оказывающих влияние на изучаемый процесс. Соотношение между масштабными множителями (индикаторы подобия) получают на основании критериев подобия изучаемого явления. На основе критериев подобия (33) для моделирования работы сооружения на грунтовом основании получены следующие индикаторы подобия:
|
|
(34) |
где ![]() - масштабный
множитель напряжений материала (или материалов) сооружения;
- масштабный
множитель напряжений материала (или материалов) сооружения;
![]() - масштабный
множитель нормальных контактных напряжений грунта (или грунтов) основания;
- масштабный
множитель нормальных контактных напряжений грунта (или грунтов) основания;
![]() - масштабный
множитель деформаций материала (или материалов) сооружения;
- масштабный
множитель деформаций материала (или материалов) сооружения;
![]() - масштабный
множитель линейных размеров;
- масштабный
множитель линейных размеров;
![]() - масштабный
множитель осадок сооружения;
- масштабный
множитель осадок сооружения;
![]() - масштабный
множитель коэффициента (или коэффициентов) Пуассона для сооружения;
- масштабный
множитель коэффициента (или коэффициентов) Пуассона для сооружения;
![]() - масштабный
множитель коэффициента (или коэффициентов) Пуассона для основания;
- масштабный
множитель коэффициента (или коэффициентов) Пуассона для основания;
![]() - масштабный
множитель коэффициентов трения по контактной поверхности сооружения и
основания.
- масштабный
множитель коэффициентов трения по контактной поверхности сооружения и
основания.
3.1.3. Для моделирования внутренних усилий в элементах сооружения необходимо выполнение условий:
|
|
(35) |
где ![]() - масштабный
множитель нормальной силы;
- масштабный
множитель нормальной силы;
![]() - масштабный
множитель изгибающего момента;
- масштабный
множитель изгибающего момента;
![]() - масштабный множитель перерезывающей
силы;
- масштабный множитель перерезывающей
силы;
![]() - масштабный
множитель крутящего момента.
- масштабный
множитель крутящего момента.
3.1.4. Для моделирования внешних силовых факторов необходимо выполнение следующих условий:
|
|
(36) |
где ![]() - масштабный
множитель сосредоточенной силы;
- масштабный
множитель сосредоточенной силы;
![]() - масштабный множитель погонной
нагрузки;
- масштабный множитель погонной
нагрузки;
![]() - масштабный множитель равномерно
распределенной нагрузки;
- масштабный множитель равномерно
распределенной нагрузки;
![]() - масштабный множитель моментной нагрузки.
- масштабный множитель моментной нагрузки.
3.1.5. Объединив выражения (34), (35) и (36), получаем условия моделирования напряженно-деформированного состояния сооружения на грунтовом основания:
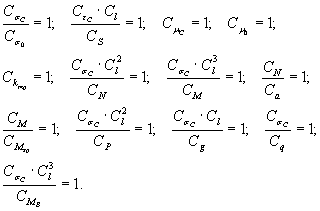
3.1.6. Исходя из того, что масштабных множителей 16, а уравнений 13, тремя масштабными множителями необходимо задаться произвольно. Из возможных вариантов наиболее приемлемые следующие два:
задаться масштабным множителем линейных размеров и масштабными множителями напряжений и деформаций материалов сооружения:
задаться масштабным множителем линейных размеров и масштабными множителями контактных напряжений и осадок основания.
В первом случае, приняв Сl, ![]() ,
, ![]() на основами (36), получаем значения
для
на основами (36), получаем значения
для ![]() , СS,
, СS, ![]() ;
; ![]() ,
, ![]() , CH, CM,
Cа,
, CH, CM,
Cа, ![]() , CP, Cg,
, CP, Cg,
![]() .
.
Во втором случае, приняв Cl, ![]() , CS на основании (36)
получаем значения для
, CS на основании (36)
получаем значения для ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . СN,
CM, Ca,
. СN,
CM, Ca, ![]() . CP.
Сg, Cq,
. CP.
Сg, Cq, ![]() .
.
3.1.7. Масштабные
множители ![]() и
и ![]() устанавливаем на
основании подобия диаграмм σ - ε материалов оригинала и модели,
получаемые на основании испытаний общепринятых образцов для каждого из
материалов,
устанавливаем на
основании подобия диаграмм σ - ε материалов оригинала и модели,
получаемые на основании испытаний общепринятых образцов для каждого из
материалов,
3.1.8. Масштабные
множители ![]() и СS устанавливаем
исходя из подобия графиков Р - S материала
основания оригинала и модели, получаемых в результате штамповых испытаний.
и СS устанавливаем
исходя из подобия графиков Р - S материала
основания оригинала и модели, получаемых в результате штамповых испытаний.
3.2. Исходная информация для установления подобия материалов оригинала и модели
3.2.1. В соответствии с положениями, изложенными в 2.1. исходной информацией для установления подобия материалов оригинала и модели грунтового основания при моделировании напряженно-деформированного состояния сооружения на грунтовом основании является подобие графиков Р - S штамповых испытаний. Графики штамповых испытаний используются в качестве исходной информации как для фундаментов под отдельно стоящие колонны, так и для ленточных фундаментов значительных размеров, а также различных их сочетаний. Отклонение от линейной зависимости осадки фундамента от площади учтено при получении критериев подобия для основания.
3.2.2. Методика проведения штамповых испытаний, за исключением формы и размеров штампа, должна соответствовать ГОСТ 12374-77 "Грунты. Метод полевого испытания статическими нагрузками".
3.2.3. Учитывая то, что под круглым штампом при центральном приложении нагрузки возникаем осесимметричное напряженно-деформированное состояние, в наиболее общем случае моделирования работы сооружения на грунтовом основании исходную информацию для установления подобия основания необходимо получать из испытаний грунтовых оснований квадратными штампами.
3.2.4. При круглых в плане фундаментах в качестве исходной информации для установления подобия грунтовых оснований возможно использование графиков Р - S испытаний круглых штампов [17].
3.2.5. Коэффициент трения подошвы штампов по поверхности основания должен быть равен коэффициенту трения подошвы натурного фундамента по поверхности основания.
3.2.6. При проведении испытаний отметка подошвы штампа должна соответствовать отметке заложения фундамента сооружения.
3.2.7. Область распределения полученных результатов штамповых испытаний на площадь строительной площадки определяют как при помощи дополнительных штамповых испытаний или других полевых методов, так и при помощи лабораторных методов исследований.
3.2.8. В общем случае исходной информацией для установления подобия материалов основания оригинала и модели при моделировании напряженно-деформированного состояния сооружения на грунтовом основании служат графики Р - S испытаний ряда различных штампов, размеры которых охватывают всю зону применения влияния размера фундаментов на осадку.
3.2.9. Учитывая то, что фундаменты шириной менее 500 мм в практике строительства встречается редко, для получения графиков Р - S натурного материала основания следует использовать штампы с размером стороны не менее 500 мм.
3.2.10. При исследовании на моделях напряженно-деформированного состояния сооружения на грунтовом основании с использованием фундаментов под отдельно стоящие колонны или ленточных фундаментов, то есть фундаментов шириной не более 7 м, в качестве исходной информации для установления подобия материалов основания оригинала и модели следует принимать графики Р - S натурного основания двух штампов размером в1 и в2 или в1 и в6 (см. рис. 6).
3.2.11. Для фундаментов под отдельно стоящие колонны и ленточных фундаментов исходной информацией может быть график Р - S одного штампа шириной, равной ширине фундамента.
3.2.12. При фундаментах значительных размеров в плане в качестве исходной информации для моделирования работы основания следует принимать графики Р - S испытаний штампов размером в4 и в5 (см. рис. 6), то есть шириной не менее 10 м.
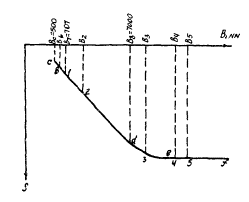
Рис. 6. Зависимость осадки штампа от его линейных размеров при постоянном давлении
3.2.13. В том случае, если сооружение находится на фундаментах под отдельно стоящие колонны, ленточных и фундаментах значительных размеров, качестве исходной информации для установления подобия материалов основания оригинала и модели следует считать графики Р - S натурного основания, как минимум, пяти штампов (см. рис. 6), из которых два должны иметь размеры, где зависимость осадки от размера штампа носит линейный характер (в1 и в2) один штамп размером в3, где зависимость между осадной и размером штампа нелинейна, два штампа размером в4 и в5, где осадка не зависит от размера штампа. Если же такая точность исходной информации недостаточна для предполагаемых исследований на моделях, количество штампов различных размеров следует увеличить.
3.2.14. В том случае, если известен график Р - S для фундамента оригинала, за исходную информацию работы основания принимается эта же зависимость осадки от давления. Наличие таких данных о натурном основании значительно упрощает получение материала основания модели, позволяющего моделировать напряженно-деформированное состояние сооружения на грунтовом основании.
3.2.15. Исходной информацией для установления подобия материалов сооружения являются диаграммы σ - ε, получаемые на основании испытаний стандартных образцов.
3.2.16. Прочность сцепления арматуры с бетоном оценивается сопротивлением выдергиванию или вдавливанию арматурных стержней, заделанных в бетоне [18]. Учитывая то, что отечественными нормами образцы на выдергивание (вдавливание) не регламентируются, можно рекомендовать получившие наибольшее распространение образцы в виде призм сечением 14×14 см и длиной от 5d до 50d (d - диаметр арматурного стержня).
3.3. Определение параметрических точек, на графике штамповых испытаний
3.3.1. Для определения координат параметрических точек могут быть рекомендованы интуитивный, частично формализованный и статистический методы.
3.3.2. При частично формализованном методе за координаты точки А, разделяющей работу основания на линейную и нелинейную, согласно [17] можно принимать значения Pi и Si, если при равных приращениях давление на штамп осадка за ступень нагружения i +1 в два раза больше, чем за ступень нагружения i. При этом приращение осадки за ступень i + 2 должно быть равно или больше приращения осадки за ступень i + 1.
3.3.3. За координаты параметрической точки В, являющейся нижней границей нелинейной стадии работы основания, при частично формализованном подходе в соответствии с [19, 20] можно принимать величину нагрузки на штамп Pi, после которой приращение осадки при увеличении давления на 0,1 кгс/см2 превышает в 3 раза приращение осадки предыдущей ступени и соответствующую ей осадку Si.
3.3.4. Координаты параметрической точки С, характеризующей нижнюю границу стадии разрушения основания, при частично формализованном подходе определяются визуально по графику штамповых испытаний.
3.3.5. Статистический метод определения координат параметрических точек основан на проверке гипотезы о равенстве средних [21, 22]. Из графиков штамповых испытаний (см. рис. 1) видно, что участки ОА и ВС линейны либо близки к линейным. Отсюда вытекает, что для участка ОА графиков Р - S при равных величинах ступеней нагружения штампа приращения осадок за ступень нагружения должны быть статистически равны.
Это же относится и к участку ВС.
3.3.6. Статистический метод определения координат параметрических точек требует наличия не менее трех графиков штамповых испытаний одного и того же основания.
3.3.7. При определении координат параметрической точки А статистическим методом поиск осуществляется по ступеням нагружения штампа в направлений, указанном стрелкой на рис. 7, от начала координат.
3.3.8. В качестве параметрической точки А принимается точка с координатами Pi-1, Si-1, для которой выполняется условие:
|
|
(38) |
или
|
|
(39) |
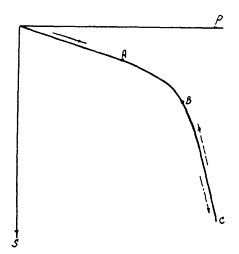
Рис. 7. Направление движения по диаграмме Р - S при определении координат параметрических точек
![]() - при определении координат точки А;
- при определении координат точки А;
![]() - при определении координат
точки В;
- при определении координат
точки В;
![]() - при определении координат точки С
- при определении координат точки С
где ![]() - среднее значение
приращения осадки за i-ю
ступень нагружения штампа;
- среднее значение
приращения осадки за i-ю
ступень нагружения штампа;
![]() -
среднее значение приращения осадки за предыдущие сравниваемые ступени
нагружения, предшествующие i-й;
-
среднее значение приращения осадки за предыдущие сравниваемые ступени
нагружения, предшествующие i-й;
ni - число элементов выборки значений приращения осадки за i-ю ступень нагружения штампа;
ni-1 - число элементов выборки значений приращения осадки за предыдущие сравниваемые ступени нагружения штампа, предшествующие i-й;
![]() - оценка дисперсии выборки пi;
- оценка дисперсии выборки пi;
![]() - оценка дисперсии выборки ni-1;
- оценка дисперсии выборки ni-1;
S - среднеквадратическое отклонение;
t1, ti, ti-1 - критерии Стьюдента, определяемые по таблицам [21, 22].
3.3.9. Условие (38)
принимается в случае равенства оценок дисперсий ![]() и
и ![]() , которое оценивается по критерий Фишера [21]. При
, которое оценивается по критерий Фишера [21]. При ![]() >
> ![]() для оценки
равенства дисперсий имеет место соотношение:
для оценки
равенства дисперсий имеет место соотношение:
|
|
(40) |
Значение критерия Фишера F принимаем по таблицам [21, 22 ] в соответствии с числом степеней свободы.
3.3.10. В случае выполнения условия (40) значение среднеквадратичного отклонения S определяется по формуле:
|
|
(41) |
где fi = ni-1; fi-1 = ni-1 - 1.
3.3.11. Если условие (40) не выполняется, для определения координат параметрической точки А принимается зависимость (39).
3.3.12. При определении координат параметрической точки В поиск начинается от любой точка линейного участка ВС графика Р - S в направлений вверх (см. рис. 7) от выбранной точки.
3.3.13. В качестве параметрической точки В принимаемся точка с координатами Pi-1, Si-1, для которой выполняется соотношение (38) или (39). Присвоение значений индекса при Р и S следует начинать с принятой отправной точки на участке ВС графика Р - S.
3.3.14. При определений координат параметрической точки С поиск начинается, как и в п:3.3.12, от любой точки линейного участка ВС графика Р - S, но в направлении вниз (см. рис. 7) от выбранной точки.
3.3.15. В качестве параметрической точки С принимается точка с координатами Pi-1, Si-1, для которой выполняется соотношение (38) или (39). Присвоение значений индекса при Р и S следует начинать с принятой отправной точки на участке ВС графика Р - S.
3.3.16. Определение параметрических точек на графике Р - S для материала основания оригинала и модели следует производить по одной и той же методике.
3.3.17. Из приведенных методов определения параметрических точек более точный статистический. Однако для ускорения процесса поиска можно рекомендовать использование интуитивного и частично формализованного методов для предварительного определения координат параметрических точек. Уточнение следует производить статистическим методом.
3.4. Получение материала основания модели
3.4.1. К материалам основания модели системы "сооружение-основание" предъявляются следующие требования:
выполнение критериев подобия и масштабных множителей удельного давленая и осадки;
постоянство во времени или на протяжении определенного промежутка времени характеристик основания;
разрушение материала не должно быть хрупким;
материал должен быть технологичным в отношений получения и укладки основания.
3.4.2. Критерий подобия материала основания определяется по графикам Р - S материала натурного основания в соответствии с п. 2.1 настоящих рекомендаций.
3.4.3. Масштабные множители удельного давления и осадки определяются в соответствии с п. 3.1.2 настоящих рекомендаций.
3.4.4. В качестве материала основания модели можно использовать песок, высушенную и измельченную глину, вспученный перлитный песок, пылеватый базальтовый песок, древесные опилки, различные золы, резину, резиновую крошку, тальк, мел, чугунную стружку, металлические и стеклянные шарики различных диаметров, молотую слюду.
3.4.5. Для получения материала основания модели могут быть использованы однокомпонентные материалы или смеси материалов, указанных в п. 3.4.4 настоящих рекомендаций.
3.4.6. Помимо данных, указанных в пп. 3.4.2 - 3.4.5, для подобия материала основания модели необходимы набор моделей штампов, размеры которых устанавливаются в соответствии с масштабным множителем линейных размеров, и расчетный график Р' - S' материала основания модели, полученный в соответствии с данными п. 3.4.2 и 3.4.3 настоящих рекомендаций.
3.4.7. Штамповые испытания следует проводить в лотках, размеры которых не оказывают влияние на результаты испытаний, Определяющий фактор при выборе размера лотка - плотность материала основания и размер штампа. Мощность слоя основания в лотке должна составлять 3 - 5 ширин штампа. Наименьший размер в плане лотка должен составлять 7 - 10 ширин штампа
3.4.8. Величина ступеней нагружения модели штампа определяется из условий простого подобия и в дальнейшем, при необходимости, корректируется.
3.4.9. При подборе материала основания модели из однокомпонентного материала следует вначале на основании априорной информации или данных предварительных экспериментальных исследований установить, что в результате изменения плотности материала или величины пригруза по поверхности основания вокруг штампа расчетные параметры нужного материала основания модели находятся внутри выявленной области. Затем, варьируя плотностью материала или величиной пригруза поверхности основания, или двумя этими факторами вместе, уже в пределах известной области получаем нужный материал. Пригруз материала основания производится сыпучим материалом.
3.4.10. Возможность применения того или иного материала в качестве составляющей части смеси определяется на основе расположения параметрических точек на графике Р - S для данного компонента или на основе выяснения влияния ее на параметры другого, принятого в качестве исходного. Материалы можно использовать в качестве компонент смеси только в том случае, если их графики Р - S образуют область, в которую попадает расчетный график Р - S материала основания модели (рис. 8).
3.4.11. При подборе материала модели основания в виде смеси варьируется процентное содержание по объему компонент смеси или по весовым частям. В том случае, если получить материал модели из принятых компонент не удается, вводятся дополнительные, позволяющие получить нужный материал.
3.4.12. Как и в случае подбора однокомпонентного материала, при получении многокомпонентного для выполнения требуемых параметров можно использовать варьирование плотности смеси.
3.4.13. В ряде случаев в качестве основания модели возможно применение основания оригинала. При этом исследования моделей должны проводиться в тех же условиях, что и натуры. В этом случае целесообразно применять крупномасштабные модели (М 1:4 - 1:2), выполненные из материалов, тождественных натурным.
3.4.14. При подборе модели в соответствии с пп. 3.4.9 - 3.4.11 настоящих рекомендаций необходимо выполнить большой объем экспериментальных работ при варьировании многих факторов (плотность, содержание компонент, размер штампа и т.д.). С целью сокращения объема экспериментальных исследований и повышения количества информации для подбора материала модели, основания, может быть применен аппарат МПЭ [22-25].
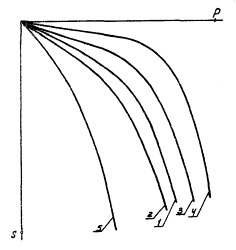
Рис. 8. Диаграммы Р - S материалов, используемых для получения модельного основания
1 - расчетный график Р - S. материала модели; 2, 3, 4, 5 - графики P - S компонент материала модели
3.4.15. Выбор факторов и уровней их варьирования осуществляется на основании априорной информации, предварительных экспериментальных исследований, интуитивно. Число факторов должно быть равно или больше числа искомых параметров.
3.4.16. При подборе материала основания модели до одному графику Р - S в качестве факторов используются компоненты смеси, плотность материала, удельная величина пригруза поверхности основания.
3.4.17. При подборе материала основания модели по двум графикам Р - S в качестве факторов используются те же составляющие факторного пространства, что и при подборе по одному графику, плюс размер штампа. Нижний уровень варьирования размера штампа при этом соответствует меньшему штампу, а верхний - большему.
3.4.18. Подбирая материал по трем и более графикам Р - S, необходимо в качестве нижнего уровня варьирования размера штампа принять наименьший из данного ряда штампов модели, в качестве верхнего уровня - наибольший.
3.4.19. Выбрав матрицу планирования в соответствии с количеством используемых факторов (см. приложение 1), необходимо провести экспериментальные исследования в соответствии с принятой матрицей планирования. Количество параллельных опытов должно быть не менее трех, Результатами реализации матрицы планирования являются значения функций отклика (характеристик основания, интересующих исследователя) для каждого из реализованных опытов.
3.4.20. Результатами обработки экспериментальных данных являются математические модели влияния варьируемых факторов на характеристики материала основания, представленные полиномиальными уравнениями вида:
|
|
(42) |
Коэффициенты уравнения регрессии определяются по формулам:
|
|
(43) |
где N - количество опытов по матрице планирования;
n - число параллельных опытов;
и - строка матрицы планирования;
к - число факторов.
3.4.21. В соответствии с положениями аппарата математической статистики [22 - 25] после получения математических моделей производится их статистический анализ. Формулы для проведения статистического анализа уравнений приведены в приложении 2.
3.4.22. Выполнив статистический анализ уравнений регрессии, получаем математические модели, позволяющие выявить влияние факторов на функции откликов (координаты параметрических и дополнительных точек, коэффициент Пуассона). Для каждой из функций откликов получаем уравнение вида (42), а влияние факторов на изменение расчетных параметров основания модели в целом описываются системой уравнений:
|
|
(44) |
В системе (44) приведены уравнения только для координат параметрических точек. При использовании дополнительных точек количество уравнений в (44) увеличивается.
3.4.23. Значения варьируемых факторов (содержание компонент смеси, плотность и т.д.) определяются из решения системы уравнений (44) после подстановки в нее расчетных параметров материала основания модели (п. 3.4.6 настоящих рекомендаций).
3.4.24. Б случае, если полученные значения факторов выходят за принятые уровни варьирования, необходимо провести дополнительные экспериментальные исследования по подтверждению математических моделей за рамками исследованного факторного пространства.
3.4.25. При подборе материала основания по двум графикам Р - S необходимо в каждое уравнение системы вида (44) подставить (вначале нижний уровень варьирования размера штампа, а затем верхний). Таким образом, получим систему уравнений:
|
|
(45) |
Продолжение формулы
|
|
|
Система уравнений (45) составлена в предположении, что фактором Х1 обозначен размер штампа.
3.4.26. Подставив в левые
части первой половины уравнений системы (45) вместо ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() расчетные величины
расчетные величины ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]()
![]() , а в левые части второй половины уравнений
, а в левые части второй половины уравнений ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]()
![]() , получаем систему уравнений, решение которой дает значения
факторов, позволяющих получить материал модели основания. Система (45) может
содержать количество уравнений больше, чем количество факторов. В этом случае
из всех возможных решений системы уравнений выбираются те, которые наиболее
полно удовлетворяют расчетным параметрам материала модели основания.
, получаем систему уравнений, решение которой дает значения
факторов, позволяющих получить материал модели основания. Система (45) может
содержать количество уравнений больше, чем количество факторов. В этом случае
из всех возможных решений системы уравнений выбираются те, которые наиболее
полно удовлетворяют расчетным параметрам материала модели основания.
3.4.27. При подборе материала основания модели по трем и более графикам Р - S необходимо вначале выполнить п.3.4.25, 3.4.26 настоящих рекомендаций. Затем, подставив полученные значения факторов в систему (44), получим систему уравнений с одной переменной - размер штампа - и определим значение функции отклика для штампов, которые не входили в матрицу планирования. Если полученные значения функции отклика совпадают с расчетными, то материал можно использовать в качестве основания модели. Если же не совпадают, то для получения нужного материала следует изменить либо уровни, либо интервал варьирования, либо сами факторы.
3.4.28. Материал модели грунтового основания можно использовать в исследованиях на моделях, в том случае, если его графики Р - S адекватны требуемым.
Приложение
1
ПРИМЕРЫ
Пример 1. При помощи исследований на моделях определим перемещения и изгибающие моменты в заданных сечениях балок постоянного сечения на грунтовом основании от действия сосредоточенной силы Р = 50 кгс, приложенной в центре пролета балки. Геометрические размеры балки и нумерация сечений приведены на рис. 1. Материал балки Ст.3. Грунтовое основание - мелкозернистый воздушно-сухой песок γ = 1,65 т/м3.
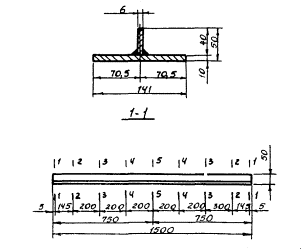
Рис.1. Геометрические размеры балки и нумерация сечений
В соответствии с п. 3.2.11 настоящих методических рекомендаций для изучения на моделях работы данной конструкции на грунтовом основании исходной информацией о работе натурного грунтового основания являются штамповые испытания с размером штампа, равным ширине балки, то есть штамп размерами 141×141мм.
Данные штамповых испытаний натурного основания приведены в таблицах 1 - 3.
Учитывая, что от заданной нагрузки материал конструкции должен работать - в упругой стадии, не налагая тем самым жестких требований на выбор материала модели, принимаем для натурной модели балки дюраль Д16Т.
Масштаб линейных размеров модели, исходя из имеющегося оборудования и точности измерительной аппаратуры, принимаем равным 1:2.
Произвольно принимаем масштабный множитель напряжений в балке,
![]()
Зная, что
![]() ,
,
и масштабный множитель модуля упругости материалов балки
СЕ = 0,3566,
определяем значение
Таблица 1
|
№ п.п. |
Р (кгс/см2) |
S (мм) |
ΔS |
|
0 |
0 |
0 |
0,475 |
|
1 |
0,0176 |
0,475 |
1,0458 |
|
2 |
0,0568 |
1,5208 |
1,0841 |
|
3 |
0,0960 |
2,5549 |
1,1067 |
|
4 |
0,1352 |
3,6616 |
1,0817 |
|
5 |
0,1744 |
4,7433 |
1,415 |
|
6 |
0,2136 |
6,1583 |
1,7617 |
|
7 |
0,2528 |
7,92 |
1,9617 |
|
8 |
0,2920 |
9,8817 |
2,0992 |
|
9 |
0,3312 |
11,9809 |
2,2767 |
|
10 |
0,3704 |
14,2576 |
2,9438 |
|
11 |
0,4096 |
17,2009 |
3,2483 |
|
12 |
0,4488 |
20,4492 |
3,3067 |
|
13 |
0,4880 |
23,7559 |
3,4542 |
|
14 |
0,5272 |
27,2101 |
3,6000 |
|
15 |
0,5664 |
30,8101 |
3,7767 |
|
16 |
0,6056 |
34,5868 |
3,4175 |
|
17 |
0,6448 |
38,0043 |
3,5608 |
|
18 |
0,6840 |
41,5651 |
3,5308 |
|
19 |
0,7232 |
45,0959 |
3,6525 |
|
20 |
0,7624 |
48,7484 |
3,6983 |
|
21 |
0,8016 |
52,4467 |
|
Таблица 2
|
№ п.п. |
Р (кгс/см2) |
S (мм) |
ΔS |
|
0 |
0 |
0 |
0,4733 |
|
1 |
0,0176 |
0,4733 |
1,1333 |
|
2 |
0,0568 |
1,6066 |
1,0433 |
|
8 |
0,0960 |
2,6499 |
1,0425 |
|
4 |
0,1352 |
3,6924 |
1,1241 |
|
5 |
0,1744 |
4,8165 |
1,385 |
|
6 |
0,2136 |
6,2015 |
1,4908 |
|
7 |
.0,2528 |
7,6923 |
1,6708 |
|
8 |
0,2920 |
9,3631 |
1,6783 |
|
9 |
0,3312 |
11,0414 |
2,1850 |
|
10 |
0,3704 |
13,2264 |
2,3583 |
|
11 |
0,4096 |
15,5847 |
2,5400 |
|
12 |
0,4488 |
18,1247 |
3,1233 |
|
13 |
0,4880 |
21,2480 |
3,0350 |
|
14 |
0,5272 |
24,2830 |
3,2375 |
|
15 |
0,5664 |
27,5205 |
3,2291 |
|
16 |
0,6056 |
30,7496 |
3,3308 |
|
17 |
0,6448 |
84,0804 |
3,3183 |
|
18 |
6,6840 |
37,3987 |
3,2400 |
|
19 |
0,7232 |
40,6387 |
3,7641 |
|
20 |
0,7624 |
44,4028 |
3,4733 |
|
21 |
0,8016 |
47,8761 |
|
Таблица 3
|
№ п.п. |
Р (кгс/см2) |
S (мм) |
ΔS |
|
0 |
0 |
0 |
0,4717 |
|
1 |
0,0176 |
0,4717 |
1,0558 |
|
2 |
0,0568 |
1,5275 |
1,0683 |
|
3 |
0,0960 |
2,5958 |
1,0283 |
|
4 |
071352 |
3,6241 |
1,07 |
|
5 |
0,1744 |
4,6941 |
1,1183 |
|
6 |
0,2136 |
5,8124 |
1,2367 |
|
7 |
0,2528 |
7,0491 |
1,5442 |
|
8 |
0,2920 |
8,5933 |
1,6588 |
|
9 |
0,3312 |
10,2516 |
2,0175 |
|
10 |
0,3704 |
12,2691 |
2,2883 |
|
11 |
0,4096 |
14,5574 |
2,7567 |
|
12 |
0,4488 |
17,3141 |
3,1042 |
|
13 |
0,4880 |
20,4183 |
3,4892 |
|
14 |
0,5272 |
23,9075 |
3,7392 |
|
15 |
0,5664 |
27,6467 |
3,45 |
|
16 |
0,6056 |
31,0967 |
3,47 |
|
17 |
0,6448 |
34,5667 |
3,5975 |
|
18 |
0,6840 |
38,1642 |
3,7425 |
|
19 |
0,7232 |
41,9067 |
3,4167 |
|
20 |
0,7624 |
45,3234 |
3,465 |
|
21 |
0,8016 |
48,7884 |
|
![]() .
.
В соответствии с п. 3.1.2
настоящих рекомендаций определяем масштабные множители удельного давления и
осадки ![]() =
= ![]() = 0,1; CS =
= 0,1; CS = ![]() ·Сl = 0,280×0,5 = 0,140.
·Сl = 0,280×0,5 = 0,140.
В результате обработки данных штамповых испытаний основания оригинала в соответствии с п. 3.3.7, 3.3.8 и 3.3.12, 3.3.13 настоящей работы при 5 %-ном уровне значимости получены координаты параметрических точек А и В.
РУ = 0,1744 кгс/см2; Sу = 4,7513 мм;
РУП = 0,4488 кгс/см2; Syn = 18,6293 мм.
Дня повышения точности исследований в нелинейной стадии работы основания (см. п. 2.1.13) введем три дополнительные точки на графике Р - S с координатами
P1 = 0,2136 кгс/см2; Р2 = 0,2528 кгс/см2; Р3 = 0,3312 кгс/см2;
S1 = 6,0574 мм; S2 = 7,5538 мм; S3 = 11,0913 мм.
Представив координаты параметрических и дополнительных точек графика Р - S в соответствии с п. 2.1.15 рекомендаций в безразмерном виде и дополнив их значениями коэффициента Пуассона и коэффициента трения по контактной поверхности, получим критерии подобия грунтового основания в виде:
![]() = 0,3886;
= 0,3886; ![]() = 0,4759;
= 0,4759; ![]() = 0,5633;
= 0,5633; ![]() = 0,7380
= 0,7380
![]() =
0,2550;
=
0,2550; ![]() = 0,3252;
= 0,3252; ![]() = 0,4055;
= 0,4055; ![]() = 0,3252;
= 0,3252;
μ0 = 0,30; Ктр - 0,42.
Из графиков штамповых испытаний грунтового основания оригинала и известных масштабных множителей удельного давления и осадки получаем расчетный график Р1 - S1 материала основания модели. Расчетные данные зависимости Р1 - S1 основания модели приведены в табл. 4.
Таблица 4
|
№ п.п. |
Р (кгс/см2) |
S (мм) |
ΔS |
|
0 |
0 |
0 |
0,0663 |
|
1 |
0,00176 |
0,0663 |
0,1509 |
|
2 |
0,00568 |
0,2173 |
0,1468 |
|
3 |
0,00960 |
0,3640 |
0,1483 |
|
.4 |
0,01352 |
0,5123 |
0,1529 |
|
5 |
0,01744 |
0,6652 |
0,1828 |
|
6 |
0,02136 |
0,8480 |
0,2095 |
|
7 |
0,2528 |
1,0575 |
0,2416 |
|
8 |
0,02920 |
1,2991 |
0,2537 |
|
9 |
0,03312 |
1,5528 |
0,3023 |
|
10 |
0,03704 |
1,8551 |
0,3542 |
|
11 |
0,04096 |
2,2093 |
0,4035 |
|
12 |
0,04488 |
2,6128 |
0,4402 |
|
13 |
0,04880 |
3,053 |
0,4657 |
|
14 |
0,05272 |
3,5187 |
0,4936 |
|
15 |
0,05664 |
4,0123 |
0,4879 |
|
16 |
0,06056 |
4,5002 |
6,4769 |
|
17 |
0,06448 |
4,9771 |
0,4889 |
|
18 |
0,06840 |
5,466 |
0,4906 |
|
19 |
0,07232 |
5,9566 |
0,5055 |
|
20 |
0,07624 |
6,4621 |
0,4964 |
|
21 |
0,08016 |
6,9585 |
|
На основании априорной информации (рис. 2) и в соответствии с п. 3.4.10 рекомендаций в качестве компонент материала основания модели приняты перлит и песок (материал основания оригинала).
При проведении предварительных экспериментальных исследований по определению уровней варьирования компонент смеси установлено, что смесь, состоящая по объему из 50 % перлита и 50 % песка (результаты штамповых испытаний приведены в таблицах 5 - 7) имеет следующие критерии подобия:
![]() = 0,415;
= 0,415; ![]() = 0,476;
= 0,476; ![]() = 0,563;
= 0,563; ![]() = 0,738
= 0,738
![]() = 0,350;
= 0,350; ![]() = 0,415;
= 0,415; ![]() = 0,468;
= 0,468; ![]() = 0,717;
= 0,717;
μ0 = 0,30; Ктр - 0,40.
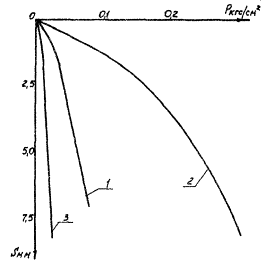
Рис. 2. Графики Р - S материалов, используемых для получения материала основания модели.
1 - расчетный график Р - S основания модели; 2 - график штамповых испытаний песка; 3 - график штамповых испытаний перлита
Сравнивая эти критерий с требуемыми, приходим к заключению, что они близки между собой и данный материал с определенными допущениями можно рассматривать как подобный натурному материалу основания.
Таблица 5
|
№ п.п. |
Р (кгс/см2) |
S (мм) |
ΔS |
|
0 |
0 |
0 |
0,165 |
|
1 |
0,00503 |
0,165 |
0,13 |
|
2 |
0,009054 |
0,295 |
0,14 |
|
3 |
0,01378 |
0,435 |
0,135 |
|
4 |
0,0172 |
0,57 |
0,165 |
|
5 |
0,02113 |
0,735 |
0,17 |
|
6 |
0,02515 |
0,905 |
0,17 |
|
7 |
0,02917 |
1,075 |
0,18 |
|
8 |
0,0332 |
1,255 |
0,175 |
|
9 |
0,03722 |
1,43 |
0,18 |
|
10 |
0,04125 |
1,61 |
0,2 |
|
11 |
0,04527 |
1,81 |
0,21 |
|
12 |
0,04929 |
2,02 |
0,21 |
|
13 |
0,05332 |
2,23 |
0,225 |
|
14 |
0,05734 |
2,455 |
0,22 |
|
15 |
0,06137 |
2,675 |
0,22 |
|
16 |
0,06539 |
2,895 |
0,225 |
|
17 |
0,06941 |
3,12 |
0,215 |
|
18 |
0,07344 |
3,345 |
|
Таблица 6
|
№ п.п. |
Р (кгс/см2) |
S (мм) |
ΔS |
|
0 |
0 |
0 |
0,15 |
|
1 |
0,00503 |
0,15 |
0,12 |
|
2 |
0,009054 |
0,27 |
0,12 |
|
3 |
0,01378 |
0,39 |
0,125 |
|
4 |
0,0171 |
0,515 |
0,16 |
|
5 |
0,02113 |
0,675 |
0,16 |
|
6 |
0,02515 |
0,895 |
0,17 |
|
7 |
0,02917 |
1,005 |
0,18 |
|
8 |
0,0332 |
1,185 |
0,175 |
|
9 |
0,03722 |
1,36 |
0,18 |
|
10 |
0,04125 |
1,54 |
0,21 |
|
11 |
0,04527 |
1,75 |
0,215 |
|
12 |
0,04929 |
1,965 |
0,22 |
|
13 |
0,05332 |
2,185 |
0,21 |
|
14 |
0,05734 |
2,385 |
0,22 |
|
15 |
0,06137 |
2,615 |
0,225 |
|
16 |
0,06539 |
2,84 |
0,22 |
|
17 |
0,06941 |
3,06 |
0,22 |
|
18 |
0,07344 |
3,28 |
|
Таблица 7
|
№ п.п. |
Р (кгс/см2) |
S (мм) |
ΔS |
|
0 |
0 |
0 |
0,175 |
|
1 |
0,00503 |
0,175 |
0,14 |
|
2 |
0,009054 |
0,315 |
0,145 |
|
3 |
0,01378 |
0,46 |
0,135 |
|
4 |
0,0171 |
3,595 |
0,17 |
|
5 |
0,02113 |
0,765 |
0,165 |
|
6 |
0,02515 |
0,93 |
0,17 |
|
7 |
0,02917 |
1,1 |
0,18 |
|
8 |
0,0332 |
1,28 |
0,18 |
|
9 |
0,03722 |
1,46 |
0,175 |
|
10 |
0,04125 |
1,635 |
0,21 |
|
11 |
0,04527 |
1,845 |
0,215 |
|
12 |
0,04929 |
2,06 |
0,22 |
|
13 |
0,05332 |
2,28 |
0,215 |
|
14 |
0,05734 |
2,495 |
0,23 |
|
15 |
0,6137 |
2,725 |
0,22 |
|
16 |
0,06539 |
2,945 |
0,23 |
|
17 |
0,06941 |
3,175 |
0,235 |
|
18 |
0,07344 |
3,41 |
|
Если исходить из координат параметрической точки В при определении масштабных множителей давления и осадок, то получим:
![]()
![]() .
.
Проверяем выполнение условия (34), приведенного в п. 3.1.2:
![]() ;
;
![]() .
.
Если исходить из координат параметрической точки А при определении масштабных множителей давления и осадки, то получим;
![]()
![]() .
.
Примем: ![]() ;
;
![]() ;
;
Поэтому условие (34) выполняется следующим образом:
![]() ;
;
![]() .
.
Сравнивая два
рассмотренных варианта, приходим к
заключению, что координаты параметрической
точки А в качестве исходных при определении ![]() и CS условия (34) выполняются более точно, чем при
использовании координат параметрической точки В. При этом достигается более
полное подобие работ материала основания в линейной фазе. Исходя из этого для
материала балки и основания принимаем следующие масштабные множители:
и CS условия (34) выполняются более точно, чем при
использовании координат параметрической точки В. При этом достигается более
полное подобие работ материала основания в линейной фазе. Исходя из этого для
материала балки и основания принимаем следующие масштабные множители:
![]() .
.
Тогда масштабный множитель для сосредоточенной силы в соответствии с п. 3.1.4 рекомендаций равен:
СР = 0,09805·0,25 = 0,0245.
Отсюда
Р1 = 50•0,0245 = 1,225 кгс.
Принимаем Р1 = 1,200 кгс.
Результаты испытаний модели балки приведены в таблицах 8 и 9.
Таблица 8
|
Нагрузка, кгс |
Вертикальные перемещения по сечениям модели балки (мм·103) |
||||
|
1-1 |
2-2 |
3-3 |
4-4 |
5-5 |
|
|
1,200 |
-0,5 |
5,667 |
14,5 |
23,0 |
27,333 |
Таблица 9
|
Нагрузка, кгс |
Изгибающие моменты в модели балки по сечениям (кгс·см) |
||
|
3-3 |
4-4 |
5-5 |
|
|
1,250 |
1,404 |
4,057 |
8,349 |
Масштабный множитель изгибающих, моментов равен См = 0,0245·0,5 = 0,01225.
Пересчет результатов испытания модели на оригинал осуществляется по формулам;
для вертикальных перемещений:
![]()
для изгибающих моментов:
![]() .
.
В таблицах 10 и 11 приведены результаты испытаний модели балки, пересчитанные на оригинал, и результаты испытаний оригинала.
Таблица 10
|
Нагрузка, кгс |
Образец |
Вертикальные перемещения балки по сечениям (мм·102) |
||||
|
1-1 |
2-2 |
3-3 |
4-4 |
5-5 |
||
|
50 |
Модель |
-0,424 |
4,809 |
12,299 |
19,51 |
23,181 |
|
Оригинал |
-2,208 |
3,083 |
11,785 |
18,79 |
23,375 |
|
Таблица 11
|
Нагрузка, кгс |
Образец |
Изгибающие моменты в балке по сечениям (кгс·см) |
||
|
3-3 |
4-4 |
5-5 |
||
|
50 |
Модель |
114,61 |
331,18 |
681,55 |
|
Оригинал |
117,62 |
330,50 |
712,50 |
|
Пример 2. Условия задачи те же, что и в примере 1.
Материалы конструкции и основания модели принимаем те же, что и для натуры, а масштаб моделирования 1:2,
Результаты штамповых испытаний основания оригинала (штамп размером 70,5×70,5) приведены в таблицах 12 - 14.
В результате обработки данных штамповых испытаний в соответствии с п. 3.3.7, 3.3.8 и 3.3.12, 3.3.13 настоящей работы при 5 %-ном уровне значимости получаем координаты параметрических точек А и В;
![]() = 0,0959 кГс/см2;
= 0,0959 кГс/см2; ![]() = 1,223 мм;
= 1,223 мм;
![]() = 0,3341 кГс/см2;
= 0,3341 кГс/см2; ![]() = 10,287 мм,
= 10,287 мм,
В соответствии с п. 2.1.15 рекомендаций имеем:
![]() = 0,287;
= 0,287; ![]() = 0,119.
= 0,119.
Сравнивая полуденные критерии с требуемыми (см. пример 1), приходим к заключению, что критерии существенно отличаются между собой. Это говорит о том, что при принятом масштабе моделирования материал основания модели не подобен материалу основания оригинала одновременно в линейной и нелинейной стадиях работы.
Вместе с тем,
рассматривая линейную стадию работы основания и используя координаты
параметрической точки А для определения ![]() и С3, получим:
и С3, получим:
![]()
![]() .
.
Принимая
![]()
и
![]()
Таблица 12
|
№ п.п. |
Р (кгс/см2) |
S (мм) |
ΔS |
|
0 |
0 |
0 |
0,215 |
|
1 |
0,0165 |
0,215 |
0,535 |
|
2 |
0,0562 |
0,750 |
0,515 |
|
3 |
0,0959 |
1,265 |
0,63 |
|
4 |
0,1356 |
1,895 |
0,91 |
|
5 |
0,1753 |
2,805 |
1,15 |
|
6 |
0,2150 |
3,955 |
1,45 |
|
7 |
0,2547 |
5,405 |
1,796 |
|
8 |
0,2944 |
7,20 |
3,225 |
|
9 |
0,3341 |
10,425 |
3,32 |
|
10 |
0,3738 |
13,745 |
3,35 |
|
11 |
0,4135 |
17,095 |
3,37 |
|
12 |
0,4532 |
20,465 |
3,70 |
|
13 |
0,4929 |
24,165 |
3,55 |
|
14 |
0,5326 |
27,715 |
3,60 |
|
15 |
0,5723 |
31,315 |
3,52 |
|
16 |
0,6120 |
34,835 |
3,55 |
|
17 |
0,6517 |
38,385 |
3,25 |
|
18 |
0,6914 |
41,635 |
|
Таблица 13
|
№ п.п. |
Р (кгс/см2) |
S (мм) |
ΔS |
|
0 |
0 |
0 |
0,19 |
|
1 |
0,0165 |
0,19 |
0,46 |
|
2 |
0,0562 |
0,65 |
0,465 |
|
3 |
0,0959 |
1,115 |
0,640 |
|
4 |
0,1356 |
1,755 |
0,960 |
|
5 |
0,1753 |
2,715 |
1,215 |
|
6 |
0,2150 |
3,93 |
1,43 |
|
7 |
0,2547 |
5,36 |
1,78 |
|
8 |
0,2944 |
7,14 |
2,94 |
|
9 |
0,3341 |
10,08 |
3,51 |
|
10 |
0,3738 |
13,59 |
3,315 |
|
11 |
0,4135 |
16,905 |
3,355 |
|
12 |
0,4532 |
20,46 |
3,35 |
|
13 |
0,4939 |
23,61 |
3,34 |
|
14 |
0,5326 |
26,95 |
3,29 |
|
15 |
0,5723 |
30,24 |
3,26 |
|
16 |
0,6120 |
33,50 |
3,32 |
|
17 |
0,6517 |
36,82 |
3,27 |
|
18 |
0,6914 |
40,09 |
|
Таблица 14
|
№ п.п. |
Р (кгс/см2) |
S (мм) |
ΔS |
|
0 |
0 |
0 |
0,22 |
|
1 |
0,0165 |
0,22 |
0,53 |
|
2 |
0,0562 |
0,75 |
0,54 |
|
3 |
0,0959 |
1,29 |
0,65 |
|
4 |
0,1356 |
1,94 |
0,85 |
|
5 |
0,1753 |
2,79 |
0,96 |
|
6 |
0,215 |
3,75 |
1,51 |
|
7 |
0,2547 |
2,56 |
2,13 |
|
8 |
0,2944 |
7,39 |
2,965 |
|
9 |
0,3341 |
10,355 |
3,56 |
|
10 |
0,3738 |
13,915 |
3,57 |
|
11 |
0,4135 |
17,485 |
3,43 |
|
12 |
0,4532 |
20,915 |
3,53 |
|
13 |
0,4529 |
24,445 |
3,49 |
|
14 |
0,5326 |
27,935 |
3,41 |
|
15 |
0,5723 |
31,345 |
3,525 |
|
16 |
0,612 |
34,87 |
3,55 |
|
17 |
0,6517 |
38,42 |
3,245 |
|
18 |
0,6914 |
41,665 |
|
проверим выполнение условия (34),
![]() ;
;
![]() .
.
Выполнение условия (34) подтверждает возможность использования материала основания оригинала в качестве модельного в линейной стадии работы основания.
На примере дополнительной точки с координатами Р3 = 0,3312 кгс/см2 и S3 = 11,0913 мм (см. пример 1) рассмотрим подобие материала основания оригинала и модели в нелинейной стадии работы. В соответствии с имеющимися масштабными множителями удельного давления и осадки получим следующие координаты дополнительной точки материала основания модели:
![]() =
0,3312×0,5499 = 0,182 кгс/см2;
=
0,3312×0,5499 = 0,182 кгс/см2;
![]() =
11,0913×0,2574 = 2,855 мм.
=
11,0913×0,2574 = 2,855 мм.
На основании данных, приведенных в таблицах 12 - 14;
![]() = 0,182 кГ/см2;
= 0,182 кГ/см2;
![]() = 2,957
мм.
= 2,957
мм.
Исходя из
вышеприведенного, приходим к выводу, что
материал модели основания подобен оригиналу не только в линейной стадии
работы материала, но и в некоторой части
нелинейной. Учитывая и величину сосредоточенной силы, прикладываемой к
балке, несмотря на нелинейность задачи, приходим к заключению, что в данном
случае материал основания оригинала можно использовать для исследований на
моделях в масштабе 1:2 при следующих масштабных множителях: ![]() = 0,5499;
= 0,5499; ![]() = 0,5499;
= 0,5499; ![]() = 0,5439; CS = 0,2574.
= 0,5439; CS = 0,2574.
Тогда масштабный множитель для сосредоточенной силы в соответствии с п. 3.1.4 настоящих рекомендаций равен СР = 0,5499·0,52 = 0,1374.
Отсюда нагрузка на модель должна быть равна Р1 =50×0,1374 = 6,87 кгс.
Принимаем Р1 = 7,00 кгс.
В таблицах 15, 16 приведены результаты испытаний модели балки на грунтовом основании.
Таблица 15
|
Нагрузка, кгс |
Вертикальные перемещения по сечениям модели балки (мм·103) |
||||
|
1-1 |
2-2 |
3-3 |
4-4 |
5-5 |
|
|
7,00 |
-6,92 |
4,08 |
26,5 |
45,92 |
55,42 |
Таблица 16
|
Нагрузка, кгс |
Изгибающие моменты по сечениям в модели в балки (кгс·см) |
||
|
3-3 |
4-4 |
5-5 |
|
|
7,00 |
10,043 |
19,958 |
43,884 |
Масштабный множитель изгибающих моментов
См = 0,1374·0,5 = 0,0687.
Пересчет результатов испытания модели на оригинал осуществляется по формулам:
для вертикальных перемещений:
![]()
для изгибающих моментов:
![]() .
.
В таблицах 17, 18 приведены результаты испытаний модели балки, пересчитанные на оригинал, и результаты испытаний оригинала.
Таблица 17.
|
Нагрузка, кГс |
Образец |
Вертикальные перемещения балки, по сечениям (мм·102) |
||||
|
1-1 |
2-2 |
3-3 |
4-4 |
5-5 |
||
|
50,00 |
Модель |
-2,687 |
1,586 |
10,295 |
17,839 |
21,530 |
|
Оригинал |
-2,208 |
3,083 |
11,785 |
18,791 |
23,375 |
|
Таблица 18
|
Нагрузка, кГс |
Образец |
Изгибающие моменты в балке по сечениям /мм·см/ |
||
|
3-3 |
4-4 |
5-5 |
||
|
50,00 |
Модель |
146,17 |
290,51 |
638,78 |
|
Оригинал |
117,62 |
330,50 |
712,50 |
|
Приложение
2
МАТРИЦЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА
(планы первого порядка)
Задача основного эксперимента - получение математической модели исследуемого объекта, которая используется для оптимизации объекта исследования или для целей аппроксимации.
Сущность факторного эксперимента первого порядка состоит в одновременном варьировании всех факторов по определенному плану, представлении математической модели в виде полинома и исследовании последнего методами математической статистики.
Введем несколько определений.
Уровнем фактора называют его определенное значение, которое фиксируется при проведении эксперимента.
Экспериментальные значения, которые могут принимать факторы, не меняя своих свойств и не искажая сути исследуемого процесса, называются границами существования факторов, а интервал (χмах - χmin) - областью их определения. При решении задачи оптимизации интервал варьирования факторов должен составлять часть области определения их. В задачах же аппроксимации (или интерполяции) интервал варьирования факторов охватывает всю описываемую область.
Для большей общности введем обозначения:
χiв - верхний уровень варьирования фактора;
χiн - нижний уровень варьирования фактора.
Уровнем фактора можно назвать и средние значения рассматриваемых интервалов. Эти значения называются нулевыми уровнями (χiо). Очевидно, что:
![]()
Такое значение фактора, прибавление которого к нулевому уровню дает верхний, а вычитание - нижний уровень, называется интервалом варьирования (Δχi).
В матрицах планирования верхние и нижние уровни варьирования факторов обозначают символами "+1" и "-1". Это соответствует кодированию их по формуле:
![]() .
.
Эксперимент с реализацией всевозможных сочетаний уровней факторов называется полным факторным экспериментом (ПФЭ) типа 2К. Каждой из строчек матрицы планирования соответствует опыт, соотношение факторов в котором определяется этой строкой. Число опытов N определяется по формуле N = 2К, где К - число факторов.
В том случае, если некоторые взаимодействия равны нулю или можно ограничиться линейным приближением зависимости отклика от независимых переменных, количество опытов по сравнению с ПФЭ можно резко сократить, используя дробный факторный эксперимент (ДФЭ), представляющий собой часть факторного пространства ПФЭ. План дробного факторного эксперимента (дробная реплика) обозначается 2К-Р, где Р - количество линейных эффектов, приравниваемых к эффектам взаимодействия. Число опытов определяется по формуле N = 2К-P.
Для построения дробных реплик используются генерирующие соотношения и определяющие контрасты. Генерирующие соотношения показывают, какое взаимодействие в матрице планирования ПФЭ с количеством факторов (к - р) заменено любым из числа Р-факторов. Соотношение, определяющее элементы первого столбца, называется определяющим контрастом. Определяющий контраст позволяет вычислить соотношения, определяющие смешанные оценки принятой дробной реплики, которые получают при умножении определяющего контраста на каждый из факторов;
Ниже приводятся матрицы планирования для 2 - 10 факторов и определяется контрасты для дробных реплик (табл. 1 - 14).
Таблица 1
К = 2
Полный факторный эксперимент
типа 22
|
Опыты |
Факторы |
Отклики |
||
|
Х0 |
Х1 |
Х2 |
||
|
1 |
+1 |
-1 |
-1 |
У1 |
|
2 |
+1 |
+1 |
-1 |
У2 |
|
3 |
+1 |
-1 |
+1 |
У3 |
|
4 |
+1 |
+1 |
+1 |
У4 |
Таблица 2
К = 3
Полный факторный эксперимент
типа 23
|
Опыты |
Факторы |
Отклики |
|||
|
Х0 |
Х1 |
Х2 |
Х3 |
||
|
1 |
+1 |
-1 |
-1 |
-1 |
У1 |
|
2 |
+1 |
+1 |
-1 |
-1 |
У2 |
|
3 |
+1 |
-1 |
+1 |
-1 |
У3 |
|
4 |
+1 |
+1 |
+1 |
-1 |
У4 |
|
5 |
+1 |
-1 |
-1 |
+1 |
У5 |
|
6 |
+1 |
+1 |
-1 |
+1 |
У6 |
|
7 |
+1 |
-1 |
+1 |
+1 |
У7 |
|
8 |
+1 |
+1 |
+1 |
+1 |
У8 |
Таблица 3
К = 4
Полный факторный эксперимент
типа 24
|
Опыты |
Факторы |
Отклики |
||||
|
Х0 |
X1 |
Х2 |
Х3 |
Х4 |
||
|
1 |
+1 |
-1 |
-1 |
-1 |
-1 |
У1 |
|
2 |
+1 |
+1 |
-1 |
-1 |
-1 |
У2 |
|
3 |
+1 |
-1 |
+1 |
-1 |
-1 |
У3 |
|
4 |
+1 |
+1 |
+1 |
-1 |
-1 |
У4 |
|
5 |
+1 |
-1 |
-1 |
+1 |
-1 |
У5 |
|
6 |
+1 |
+1 |
-1 |
+1 |
-1 |
У6 |
|
7 |
+1 |
-1 |
+1 |
+1 |
-1 |
У7 |
|
8 |
+1 |
+1 |
+1 |
+1 |
-1 |
У8 |
|
9 |
+1 |
-1 |
-1 |
-1 |
+1 |
У9 |
|
10 |
+1 |
+1 |
- |
-1 |
+1 |
У10 |
|
11 |
+1 |
-1 |
+1 |
-1 |
+1 |
У11 |
|
12 |
+1 |
+1 |
+1 |
-1 |
+1 |
У12 |
|
13 |
+1 |
-1 |
-1 |
+1 |
+I |
У13 |
|
14 |
+1 |
+1 |
-1 |
+1 |
+1 |
У14 |
|
15 |
+1 |
-1 |
+1 |
+1 |
+1 |
У15 |
|
16 |
+1 |
+1 |
+1 |
+1 |
+1 |
У16 |
Таблица 4
К = 3
Полуреплика типа 23-1
Определяющий контраст 1 = -X1 Х2 Х3
|
Опыты |
Факторы |
Отклики |
|||
|
Х0 |
X1 |
Х2 |
Х3 |
||
|
1 |
+1 |
-1 |
-1 |
-1 |
У1 |
|
2 |
+1 |
+1 |
-1 |
+1 |
У2 |
|
3 |
+1 |
-1 |
+1 |
+1 |
У3 |
|
4 |
+1 |
+1 |
+1 |
-1 |
У4 |
Таблица 5
К = 4
Полуреплика типа 24-1
Определяющий контраст = Х1 Х2 Х3 Х4
|
Опыты |
Факторы |
Отклики |
||||
|
Х0 |
X1 |
Х2 |
Х3 |
Х4 |
||
|
1 |
+1 |
-1 |
-1 |
-1 |
-1 |
У1 |
|
2 |
+1 |
+1 |
-1 |
-1 |
+1 |
У2 |
|
3 |
+1 |
-1 |
+1 |
-1 |
+1 |
У3 |
|
4 |
+1 |
+1 |
+1 |
-1 |
-1 |
У4 |
|
5 |
+1 |
-1 |
-1 |
+1 |
+1 |
У5 |
|
6 |
+1 |
+1 |
-1 |
+1 |
-1 |
У6 |
|
7 |
+1 |
-1 |
+1 |
+1 |
-1 |
У7 |
|
8 |
+1 |
+1 |
+1 |
+1 |
+1 |
У8 |
Таблица 6
К = 5
Четверть - реплика 25-2
Определяющий контраст 1 = X1 X2 X3 = X3 Х4 X5 = X1 Х2 Х3 Х4
|
Опыты |
Факторы |
Отклики |
|||||
|
Х0 |
X1 |
Х2 |
Х3 |
Х4 |
Х5 |
||
|
1 |
+1 |
-1 |
-1 |
-1 |
-1 |
+1 |
У1 |
|
2 |
+1 |
+1 |
-1 |
-1 |
+1 |
-1 |
У2 |
|
3 |
+1 |
-1 |
+1 |
-1 |
+1 |
-1 |
У3 |
|
4 |
+1 |
+1 |
+1 |
-1 |
-1 |
+1 |
У4 |
|
5 |
+1 |
-1 |
-1 |
+1 |
+1 |
+1 |
У5 |
|
6 |
+1 |
+1 |
-1 |
+1 |
-1 |
-1 |
У6 |
|
7 |
+1 |
-1 |
+1 |
+1 |
-1 |
-1 |
У7 |
|
8 |
+1 |
+1 |
+1 |
.+1 |
+1 |
+1 |
У8 |
Таблица 7
К = 5
Полуреплика 25-1
Определяющий контраст 1 = X1 Х2 Х3 Х4 Х5
|
Опыты |
Факторы |
Отклики |
|||||
|
Х0 |
X1 |
Х2 |
Х3 |
Х4 |
Х5 |
||
|
1 |
+1 |
-1 |
-1 |
-1 |
-1 |
+1 |
У1 |
|
2 |
+1 |
+1 |
-1 |
-1 |
-1 |
-1 |
У2 |
|
3 |
+1 |
-1 |
+1 |
-1 |
-1 |
-1 |
У3 |
|
4 |
+1 |
+1 |
+1 |
-1 |
-1 |
+1 |
У4 |
|
5 |
+1 |
-1 |
-1 |
-1 |
-1 |
-1 |
У5 |
|
6 |
+1 |
+1 |
-1 |
+1 |
-1 |
+1 |
У6 |
|
7 |
+1 |
-1 |
+1 |
+1 |
-1 |
+1 |
У7 |
|
8 |
+1 |
+1 |
+1 |
+1 |
-1 |
-1 |
У8 |
|
9 |
+1 |
-1 |
-1 |
-1 |
+1 |
-1 |
У9 |
|
10 |
+1 |
+1 |
-1 |
-1 |
+1 |
+1 |
У10 |
|
11 |
+1 |
-1 |
+1 |
-1 |
+1 |
+1 |
У11 |
|
12 |
+1 |
+1 |
+1 |
-1 |
+1 |
-1 |
У12 |
|
13 |
+1 |
-1 |
-1 |
+1 |
+1 |
+1 |
У13 |
|
14 |
+1 |
+1 |
-1 |
+1 |
+1 |
-1 |
У14 |
|
15 |
+1 |
-1 |
+1 |
+1 |
+1 |
-1 |
У15 |
|
16 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
У16 |
Таблица 8
К = 6
1/8 реплика типа 26-3
Определяющий контраст 1 = X1 X3 Х5 = X1 Х4 X6 = Х2 Х3 X6 = Х2 Х4 Х5 = X1, Х2 Х3 Х4 =
= X1 Х2 Х5 Х6 = Х3 Х4 Х5 X6
|
Опыты |
Факторы |
Отклики |
||||||
|
Х0 |
X1 |
Х2 |
Х3 |
Х4 |
Х5 |
Х6 |
||
|
1 |
+1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
У1 |
|
2 |
+1 |
+1 |
-1 |
-1 |
+1 |
+1 |
-1 |
У2 |
|
3 |
+1 |
-1 |
+1 |
-1 |
+1 |
-1 |
+1 |
У3 |
|
4 |
+1 |
+1 |
+1 |
-1 |
-1 |
+1 |
+1 |
У4 |
|
5 |
+1 |
-1 |
-1 |
+1 |
+1 |
+1 |
+1 |
У5 |
|
6 |
+1 |
+1 |
-1 |
+1 |
-1 |
-1 |
+1 |
У6 |
|
7 |
+1 |
-1 |
+1 |
+1 |
-1 |
+1 |
-1 |
У7 |
|
8 |
+1 |
+1 |
+1 |
+1 |
+1 |
-1 |
-1 |
У8 |
Таблица 9
К = 6
1/4 - реплика типа 26-2
Определяющий контраст 1 = X1 X2 X3 X5 = X1 X2 X4 X6 = Х3 Х4 Х5 Х6
|
Опыты |
Факторы |
Отклики |
||||||
|
Х0 |
X1 |
Х2 |
Х3 |
Х4 |
Х5 |
Х6 |
||
|
1 |
+1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
У1 |
|
2 |
+1 |
+1 |
+1 |
+1 |
-1 |
+1 |
-1 |
У2 |
|
3 |
-1 |
+1 |
+1 |
-1 |
+1 |
-1 |
+1 |
У3 |
|
4 |
+1 |
-1 |
-1 |
+1 |
+1 |
+1 |
+1 |
У4 |
|
5 |
+1 |
+1 |
-1 |
+1 |
+1 |
-1 |
-1 |
У5 |
|
6 |
+1 |
+1 |
-1 |
-1 |
-1 |
+1 |
+1 |
У6 |
|
7 |
+1 |
-1 |
+l |
+1 |
-1 |
-1 |
+1 |
У7 |
|
8 |
+1 |
-1 |
+1 |
-1 |
+1 |
+1 |
-1 |
У8 |
|
9 |
+1 |
+1 |
+1 |
-1 |
-1 |
-1 |
-1 |
У9 |
|
10 |
+1 |
-1 |
-1 |
+1 |
-1 |
+1 |
-1 |
У10 |
|
11 |
+1 |
-1 |
-1 |
-1 |
+1 |
-1 |
+1 |
У11 |
|
12 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
У12 |
|
13 |
+1 |
+1 |
-1 |
+1 |
-1 |
-1 |
+1 |
У13 |
|
14 |
+1 |
+1 |
-1 |
-1 |
+1 |
+1 |
-1 |
У14 |
|
15 |
+1 |
-1 |
+1 |
+1 |
+1 |
-1 |
-1 |
У15 |
|
16 |
+1 |
-1 |
+1 |
-1 |
-1 |
+1 |
+1 |
У16 |
Таблица 10
К = 7
1/16 - реплика типа 27-4
Определяющий контраст 1 = X1 Х2 Х7 = X1 X3 X5 = X1 X4 X6 = Х2 Х3 Х6 = Х2 Х4 Х5 = Х3 Х4 Х7 = Х5 Х6 Х7 = Х1 Х2 Х3 Х4 = Х1 Х2 Х5 Х6 = Х1 Х3 Х6 Х7 =Х1 Х4 Х5 Х7 = Х2 Х3 Х5 Х7 = Х2 Х4 Х6 Х7 = Х3 Х4 Х5 Х6 = Х1 Х2 Х3 Х4 Х5 Х6 Х7
|
Опыты |
Факторы |
Отклики |
|||||||
|
Х0 |
X1 |
Х2 |
Х3 |
Х4 |
Х5 |
Х6 |
Х7 |
||
|
1 |
+1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
У1 |
|
2 |
+1 |
+1 |
+1 |
+1 |
-1 |
+1 |
-1 |
-1 |
У2 |
|
3 |
-1 |
+1 |
+1 |
-1 |
+1 |
-1 |
+1 |
-1 |
У3 |
|
4 |
+1 |
+1 |
-1 |
+1 |
-1 |
-1 |
+1 |
+1 |
У4 |
|
5 |
+1 |
+1 |
-1 |
-1 |
+1 |
+1 |
-1 |
+1 |
У5 |
|
6 |
+1 |
-1 |
+1 |
+1 |
-1 |
+1 |
-1 |
+1 |
У6 |
|
7 |
+1 |
-1 |
+1 |
-1 |
+1 |
-1 |
+1 |
+1 |
У7 |
|
8 |
+1 |
-1 |
-1 |
+1 |
+1 |
+1 |
+1 |
-I |
У8 |
Таблица 11
К = 7
1/8 - реплика типа 27-3
Определяющий контраст 1 = Х1 Х2 Х3 Х4 = Х1 Х2 Х5 Х6 = Х1 Х3 Х5 Х7 = Х1 Х4 Х6 Х7 = Х2 Х3 Х6 Х7 = Х2 Х4 Х5 Х7 = Х3 Х4 Х5 Х6
|
Опыты |
Факторы |
Отклики |
|||||||
|
Х0 |
X1 |
Х2 |
Х3 |
Х4 |
Х5 |
Х6 |
Х7 |
||
|
1 |
2 |
3 |
4 |
5 |
.6 |
7 |
8 |
9 |
10 |
|
1 |
+1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
У1 |
|
2 |
+1 |
-1 |
-1 |
-1 |
-1 |
+1 |
+1 |
+1 |
У2 |
|
3 |
+1 |
+1 |
+1 |
+1 |
+1 |
-1 |
-1 |
-1 |
У3 |
|
4 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
У4 |
|
5 |
+1 |
+1 |
+1 |
-1 |
-1 |
-1 |
-1 |
+1 |
У5 |
|
6 |
+1 |
-1 |
-1 |
+1 |
+1 |
-1 |
-1 |
+1 |
У6 |
|
7 |
+1 |
+1 |
+1 |
-1 |
-1 |
+1 |
+1 |
-1 |
У7 |
|
8 |
+1 |
-1 |
-1 |
+1 |
+1 |
+1 |
+1 |
-1 |
У8 |
|
9 |
+1 |
+1 |
-I |
+1 |
-I |
-I |
+', |
-I |
У9 |
|
10 |
+1 |
-1 |
+1 |
-1 |
+1 |
-I |
+'. |
-I |
У10 |
|
11 |
+1 |
+1 |
-I |
+1 |
-I |
+1 |
-I |
' +1 |
У11 |
|
12 |
+1 |
-1 |
+1 |
-I |
+1 |
+1 |
-I |
+1 |
У12 |
|
13 |
+1 |
+1 |
-I |
-I |
+1 |
+1 |
-1 |
-I |
У13 |
|
14 |
+1 |
-1 |
+* |
+1 |
-I |
+1 |
-] |
' -I |
У14 |
|
15 |
+1 |
+1 |
-I |
-I |
+1 |
-I |
+'. |
+1 |
У15 |
|
16 |
+1 |
-1 |
+1 |
+Г |
-I |
-I |
+. |
+1 |
У16 |
Таблица 12
К = 8
1/16 - реплика типа 28-4
Определяющий контраст 1 = X1 X5 X6 = X2 X5 Х7 = X3 X5 X8 = X1 X2 Х4 X8 = X1 X2 X6 X7 = X1 X3 X6 X8 = X2 X3 X4 X6 = X2. X3 X7 X8 = X4 X6 X7 X8 = X1 X2 X3 X4 X5 = X1 X4 X5 X7 X8 = X2 X4 X5 X6 X8 = X3 X4 X5 X6 X7 = X1 X2 X3 X5 X6 X7, X8.
|
Опыты |
Факторы |
Отклики |
||||||||
|
Х0 |
X1 |
Х2 |
Х3 |
Х4 |
Х5 |
Х6 |
Х7 |
Х8 |
||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
1 |
+1 |
.+1 |
-1 |
-1 |
-1 |
+1 |
-1 |
-1 |
-1 |
У1 |
|
2 |
+1 |
+1 |
-1 |
-1 |
-1 |
-1 |
-1 |
+1 |
+1 |
У2 |
|
3 |
+1 |
-1 |
+1 |
-1 |
-1 |
-1 |
+1 |
-1 |
+1 |
У3 |
|
4 |
+1 |
+1 |
+1 |
-1 |
-1 |
+1 |
+1 |
+1 |
-1 |
У4 |
|
5 |
+1 |
-1 |
-1 |
+1 |
-1 |
-1 |
+1 |
+1 |
-1 |
У5 |
|
6 |
+1 |
+1 |
-1 |
+1 |
-1 |
+1 |
-1 |
-1 |
+1 |
У6 |
|
7 |
+1 |
-1 |
+1 |
+1 |
-1 |
+1 |
-1 |
+1 |
+1 |
У7 |
|
8 |
+1 |
+1 |
+1 |
+1 |
-1 |
-1 |
-1 |
-1 |
-1 |
У8 |
|
9 |
+1 |
-1 |
-1 |
-1 |
+1 |
-1 |
+1 |
+1 |
+1 |
У9 |
|
10 |
+1 |
+1 |
-1 |
-1 |
+1 |
+1 |
+1 |
-1 |
-1 |
У10 |
|
11 |
+1 |
-1 |
+1 |
-1 |
+1 |
+1 |
-1 |
+1 |
-1 |
У11 |
|
12 |
+1 |
+1 |
+1 |
-1 |
+1 |
-1 |
-1 |
-1 |
+1 |
У12 |
|
13 |
+1 |
-1 |
-1 |
+1 |
+1 |
+1 |
-1 |
-1 |
+1 |
У13 |
|
14 |
+1 |
+1 |
-1 |
+1 |
+1 |
-1 |
-1 |
+1 |
-1 |
У14 |
|
15 |
+1 |
-1 |
+1 |
+1 |
+1 |
-1 |
+1 |
-1 |
-1 |
У15 |
|
16 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
У16 |
Таблица 13
К = 9
1/32 - реплика типа 29-5
Определяющий контраст 1 = X1 X5 X6 = X2 X5 X7 = X3 X5 X8 = Х1 Х2 X3 Х9 = Х1 X2 Х4 X8 = Х1 Х2 Х6 X7 = Х1 Х3 Х4 Х7 = X1 X3 X6 X8 = X1 X4 X5 X9 = Х1 Х4 Х6 Х9 = X2 Х3 X4 X6 = X2 X3 X7 X8 = X2 X4 X7 X9 = X2 X6 X8 X9 = X3 X4 X5 X7 = X3 X4 X8 X9 = Х3 X6 X7 X8 = Х4 Х6 Х7 Х8 = X1 Х2 X3 X4 X5 = Х1 Х2 X5 X8 X9 = X1 X3 X5 X7 X9 = Х1 Х4 Х5 Х7 Х8 = X2 X3 X5 Х6 X9 = X2 X4 X5 Х6 X8 = X5 X6 X7 X8 X9 = Х1 X2 X3 X5 X6 Х7 X8 = X1 X2 X4 X5 X6 Х7 Х9 = X1 X3 X4 X5 X6 X8 X9 = X2 X3 X4 X5 X7 X8 X9 = X1 X2 X3 Х4 X6 Х7 X8 X9
|
Опыты |
Факторы |
Отклики |
|||||||||
|
Х0 |
X1 |
Х2 |
Х3 |
Х4 |
Х5 |
Х6 |
Х7 |
Х8 |
Х9 |
||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
1 |
+1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
У1 |
|
2 |
+1 |
+1 |
-1 |
-1 |
-1 |
-1 |
-1 |
+1 |
+1 |
+1 |
У2 |
|
3 |
+1 |
-1 |
+1 |
-1 |
-1 |
-1 |
+1 |
-1 |
+1 |
+1 |
У3 |
|
4 |
+1 |
+1 |
+1 |
-1 |
-1 |
+1 |
+1 |
+1 |
-1 |
-1 |
У4 |
|
5 |
+1 |
-1 |
-1 |
+1 |
-1 |
-1 |
+1 |
+1 |
-1 |
+1 |
У5 |
|
6 |
+1 |
+1 |
-1 |
+1 |
-1 |
+1 |
+1 |
-1 |
+1 |
-1 |
У6 |
|
7 |
+1 |
-1 |
+1 |
+1 |
-1 |
+1 |
-1 |
+1 |
+1 |
-1 |
У7 |
|
8 |
+1 |
+ |
+1 |
+1 |
-1 |
-1 |
-1 |
-1 |
-1 |
+1 |
У8 |
|
9 |
+1 |
-1 |
-1 |
-1 |
+1 |
-I |
+1 |
+1 |
+1 |
-1 |
У9 |
|
10 |
+1 |
+1 |
- |
-1 |
+1 |
+1 |
+1 |
-1 |
-1 |
+1 |
У10 |
|
11 |
+1 |
-1 |
+1 |
-1 |
+1 |
+1 |
-1 |
+1 |
-1 |
+1 |
У11 |
|
12 |
+1 |
+1 |
+1 |
-1 |
+1 |
-1 |
-1 |
-1 |
+1 |
-1 |
У12 |
|
13 |
+1 |
-1 |
-1 |
+1 |
+1 |
+1 |
-1 |
-1 |
+l |
+1 |
У13 |
|
14 |
+1 |
+1 |
-1 |
+1 |
+1 |
-1 |
-1 |
+1 |
-1 |
-1 |
У14 |
|
15 |
+1 |
-1 |
+1 |
+1 |
+1 |
-1 |
+1 |
-1 |
-1 |
-1 |
У15 |
|
16 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
У16 |
Таблица 14
К = 10
1/64 - реплика типа 210-6
Определяющий контраст 1 = Х1 X2 XJ0 = X1 Х5 Х6 = Х2 Х5 Х7 = Х3 Х5 Х8 = Х3 Х9 Х10 = Х4 Х5 Х9 = Х4 Х8 Х10 = Х7 Х8 Х9 = X1 Х2 Х3 Х9 = X1 Х2 Х4 Х8 = X1 Х2 X6 Х7 = X1 Х3 Х4 Х7 = X1 X3 X6 X8 = X1 X4 X6 X9 = X1 X5 X7 X10 = Х2 Х3 Х4 Х6 = Х2 Х3 Х7 Х8 = х2 х4 х7 х9 = х2 х5 х6 x10 = х2 х6 х8 х9 = X3 X4 X5 X10 = X3 X4 X8 X9 = X3 X6 X7 X9 = X4 X6 X7 X8 = X1 X2 X3 X4 X5 = X1 X2 X5 X8 X9 = X1 X3 X4 X6 X10 = X1 X3 X5 X7 X9 = X1 X3 X7, X8 X10 = X1 X4 X5 X7 X8 = X1 X4 X7 X9 X10 = X1 X6 X8 X9 X10 = X2 X3 X4 X7, X10 = X2 X3 X5 X6 X9 = X2 X3 X6 X8 X10 = X2 Х4 X5 X6 X8 = X2 X4 X6 X9 X10 = X2 X5 X8 X9 X10 = X2 X7 X8 X9 X10 = X3 X4 X5 X6 X7 = X5 X6 X7 X8 X9 = X1 X2 X3 X5 X8 X10 = X1 X2 X4 X5 X9 X10 = X1 X3 X5 X6 X9 X10 = X1 X4 X5 X6 X8 X10 = X2 X3 X5 X7 X9 X10 = X2 X4 X5 X7 X8 X10 = X3 X5 X6 X7 X8 X10 = Х4 Х5 X6 X7 X9 X10 = X1 X2 X3 Х4 X8 X9 X10 = X1 X2 X3 X5 X6 X7 X8 = X1 X2 X3 X6 X7 X9 X10 = X1 X2 X4 X5 X6 X7 X9 = X1 X2 X4 X6 X7 X9 Х10 = X1 X3 X4 X5 X6 X8 X9 =X2 X3 Х4 X5 Х7 X8 X9 = X3 X4 X6 Х7 X8 X9 X10= XI X2 X3 X4 X5 X6 X7 X10 = XI X2 X5 X6 Х7 X8 X9 X10 = X1 X3 X4 X5 Х7 X8 X9 X10 = X2 X3 X4 X5 X6 X8 X9 X10.
|
Опыты |
Факторы |
Отклики |
||||||||||
|
Х0 |
X1 |
Х2 |
Х3 |
Х4 |
Х5 |
Х6 |
Х7 |
Х8 |
Х9 |
XI0 |
||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
1 |
+1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
+1 |
У1 |
|
2 |
+1 |
+1 |
-1 |
-1 |
-1 |
-1 |
-1 |
+1 |
+1 |
+1 |
+1 |
У2 |
|
3 |
+ I |
+1 |
+1 |
-1 |
-1 |
-1 |
+1 |
-1 |
+1 |
+1 |
-1 |
У3 |
|
4 |
+1 |
+1 |
+1 |
-1 |
-1 |
+1 |
+1 |
+1 |
-1 |
-1 |
+1 |
У4 |
|
5 |
+1 |
-1 |
-1 |
+1 |
-1 |
-1 |
+1 |
+1 |
-1 |
+1 |
+1 |
У5 |
|
6 |
+1 |
+1 |
-1 |
+1 |
-1 |
+1 |
+1 |
-1 |
+1 |
-1 |
-1 |
У6 |
|
7 |
+1 |
-1 |
+1 |
+1 |
-1 |
+1 |
-1 |
-1 |
+1 |
-1 |
-1 |
У7 |
|
8 |
+1 |
+1 |
+1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
+1 |
+1 |
У8 |
|
9 |
+1 |
-1 |
-1 |
-I |
+1 |
-1 |
+1 |
+1 |
+2 |
-1 |
+1 |
У9 |
|
10 |
+1 |
+1 |
-1 |
-I |
+1 |
+1 |
+1 |
-1 |
-1 |
+1 |
-1 |
У10 |
|
11 |
+1 |
-1 |
+1 |
-I |
+1 |
+1 |
-1 |
+1 |
-1 |
+1 |
-1 |
У11 |
|
12 |
+1 |
+1 |
+1 |
-I |
+1 |
-1 |
-1 |
-1 |
+1 |
-1 |
+1 |
У12 |
|
13 |
+1 |
-1 |
-1 |
+1 |
+1 |
+1 |
-1 |
-1 |
+1 |
+1 |
+1 |
У13 |
|
14 |
+1 |
+1 |
-1 |
+1 |
+1 |
-1 |
-1 |
+1 |
-1 |
-1 |
-1 |
У14 |
|
15 |
+1 |
-1 |
+1 |
+1 |
+1 |
-1 |
+1 |
-1 |
-1 |
-1 |
-1 |
У15 |
|
16 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
У16 |
Приложение
3
ИССЛЕДОВАНИЕ ПОЛИНОМА МЕТОДАМИ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Статистический анализ уравнения регрессии состоит из оценки ошибок опыта (оценка дисперсии воспроизводимости), значимости коэффициента уравнения регрессии и оценки адекватности математической модели.
Ошибка опыта ![]() оценивается по
параллельным опытам. При определении оценки ее вначале необходимо убедиться в
однородности построчных дисперсий, определенных по формуле
оценивается по
параллельным опытам. При определении оценки ее вначале необходимо убедиться в
однородности построчных дисперсий, определенных по формуле ![]() , где п - число
параллельных опытов; и - строка
матрицы планирования;
, где п - число
параллельных опытов; и - строка
матрицы планирования; ![]() .
.
Проверка однородности дисперсии при одинаковом количестве параллельных опытов осуществляется по критерию Кохрена [21], расчетное значение которого можно представить в виде:
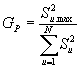 ,
,
где ![]() - максимальная из
построчных дисперсий;
- максимальная из
построчных дисперсий;
N - количество опытов (количество строк матрицы планирования).
Затем по таблицам [21] определяется табличное значение критерия Кохрена GT и проверяется выполнение условия Gр < GT.
Если данное условие
выполняется, то гипотеза об однородности построчных дисперсий принимается и
оценка ошибки опыта определяется по формуле ![]() .
.
Неоднородные дисперсии не осредняются и необходимо провести дополнительные экспериментальные исследования по уточнению значения функции отклика.
Проверка оценки значимости
коэффициентов уравнения регрессии осуществляется двумя способами. Как для
первого, так и для второго способа вначале определяет дисперсию коэффициентов
уравнения регрессии ![]() .
.
Осуществляя проверку
оценки значимости коэффициентов по первому способу, необходимо вычислить
расчетное значение критерия Стьюдента по формуле 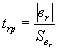 , где
, где ![]() - абсолютное значение
проверяемого коэффициента уравнения регрессии.
- абсолютное значение
проверяемого коэффициента уравнения регрессии.
По таблицам [2l] следует определить значение критерия Стьюдента tТ по числу степеней свободы f = N(n-1) и уровню значимости q. Коэффициенты уравнения регрессии значимы, если выполняется условие trp > tT.
При проверке значимости
оценки коэффициентов уравнения регрессии по второму способу используют доверительный
интервал ![]() .
.
Коэффициенты уравнения регрессии значимы, если выполняется условие:
|вr| > |Δвr|
Если в результате проверки значимости коэффициентов уравнения регрессии установлено, что некоторые коэффициенты не значимы, то их следует изъять.
Для проверки адекватности уравнения регрессии вначале необходимо вычислить дисперсию адекватности:
![]() ,
,
где С - число членов в уравнении регрессии, оставшихся после оценки значимости коэффициентов уравнения регрессии;
![]() - значение
отклика (переменного состояния), вычисленное по уравнению регрессии.
- значение
отклика (переменного состояния), вычисленное по уравнению регрессии.
Следует вычислить расчетное значение критерия Фишера:
![]()
Определил табличное значение критериев Фишера для степеней свободы fag = N•с, f0 = N(п - i)и принятого уровня значимости q по таблице [21].
Уравнение регрессии адекватно экспериментальным данным при выполнении условия FP < FT.
Если ![]() то проверка
адекватности уравнения регрессии не производится, так как в этом случае
уравнение адекватно экспериментальным данным.
то проверка
адекватности уравнения регрессии не производится, так как в этом случае
уравнение адекватно экспериментальным данным.
В результате проведенного статистического анализа получаем математическую модель, описываемую влиянием факторов исследуемого факторного пространства на характеристику основания.
ЛИТЕРАТУРА
1. Назаров А.Г., О механическом подобии твердых деформируемых тел. - АН АрмССР, Ереван, 1965.
2. Веников В.А. Теория подобия и моделирования - Киев: Вища школа, 1966.
3. Гольдштейн М.Н. Механические свойства грунтов (напряженно-деформированные и прочностные характеристики). -М.: Стройиздат, 1979.
4. Ярмульник Ф.В., Шарапов Г.В., Гайдук В.Г. Методика подбора материала при исследовании железобетонных конструкций на моделях. - Киев: Вища школа, 1974.
5. Гольдштейн М.И., Кушнер С.Г., Шевченко М.И. Расчеты осадок и прочности оснований зданий и сооружений. Киев: БудIвельник, 1977 г.
6. Горбунов-Посадов М.И., Давидов С.С. О совместной работе оснований и сооружений. Генеральные доклада VIII Международного конгресса по механике грунтов и фундаментостроения. - М.: Стройиздат, 1975.
7. Тарасюк В.Г. О выборе условий подобия для основания сооружения. - В сб.: Строительные конструкции. Вып.XXXI. -Киев: БудIвельник, 1978.
8. Цытович Н.А. Механика грунтов.- М.: Высшая школа, 1979.
9. Чижиков П.Г. Зависимости между нагрузками и осадками модельного и натурного фундаментов /Труды ЦНИИС; -М.: Госстройиздат, 1961.
10. Чижиков П.Г. Исследование прочности и осадки песчаных оснований /Труды ЦНИИС, вып.47. - М.: Трансжелдориздат, 1963.
11. Чижиков П.Р. Моделирование сопротивлений и осадок песчаных оснований в различных фазах деформаций /Труды ЦНИИС, вып.56, - М.: Транспорт, 1965.
12. Козлов В.П. О переходных коэффициентах при моделировании взаимодействия подрабатываемых сооружений с основанием на естественном грунте /Труда ДонпромстройНИЙпроекта, № 6. -М.: Недра, 1965.
13. Чижиков А.Г. К исследованию прочности и деформативности системы "фундамент-грунт" /Труды ЦНИИС, вып. 56. -М.: Транспорт, 1965.
14. Довнарович С.В., Польшин Д.Е. О выборе размера модели фундамента при моделировании осадок песчаного основания. -Основание, фундаменты и механика грунтов, 1967, № 4.
15. ГОСТ 1200-66. Сталь арматурная. Методы испытания на растяжение.
16. Тарасюк В.Г., Шарапов Г.В. Моделирование работы сооружения на грунтовом основании. -В кн.: Совершенствование методов расчета и испытаний строительных конструкций. - Киев: БудIвельник, 1980.
17. ГОСТ 12374-77. Грунты. Метод полевого испытания статическими нагрузками.
18. Байков В.Н., Сигалов Э.Е., Железобетонные конструкции. Общий курс. -М.: Стройиздат, 1976.
19. Рудницкий Н.Я., Малахова К.В. Центробежное моделирование несущей способности насыщенного водой нестабилизированного глинистого основания. - Основание, фундаменты и механика грунтов, 1976, № 6.
20. Рудницкий Н.Я., Малахова К.В. О достоверности метода центробежного моделирования деформаций оснований, сложенных глинистыми грунтами. -Основание, фундаменты и механика грунтов, 1979, № 2.
21. Пустыльник Е.И. Статические метода анализа и обработки наблюдений. - М.: Наука, 1968.
22. Бондарь А.Г., Статюха Г.А. Планирование эксперимента в химической технологии. -Киев: Вища школа, 1976.
23. Налимов В.В., Чернова Н.А. Статические методы планирования экспериментальных экспериментов. - М.: Наука, 1965.
24. Налимов В.В. Теория эксперимента. - М.: Наука, 1971.
25. Адлер Ю.П. Введение в планирование эксперимента. - М.: Металлургия, 1969.
|
|||||||||||||||||||||